Ребятушки Исследовать с производной функцию y=x^3-3x+2 и построить её график. Найти точки, в которых касательные к графику параллельны оси Ох. Найти выпуклость и перегиб.
1.3 x = - 1, y = - 2, подставляем значения в функцию, если равенство будет верным, то значит точка А(-1; - 2) принадлежит графику функции. (в 1.2 мы нашли корни уравнения, при y=-2, x=-1, значит точка принадлежит графику функции, но, всё же, распишу так: )
равенство верное, точка принадлежит графику функции.
#1. Функция задана формулой
1.1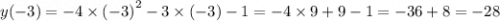
1.2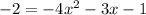
1.3 x = - 1, y = - 2, подставляем значения в функцию, если равенство будет верным, то значит точка А(-1; - 2) принадлежит графику функции. (в 1.2 мы нашли корни уравнения, при y=-2, x=-1, значит точка принадлежит графику функции, но, всё же, распишу так: )
равенство верное, точка принадлежит графику функции.
#2. Используя график функции укажите:
2.1 Область определения функции: [-4.5; 5]
2.2 Область значения функции: [-2.5; 4.5]
2.3 Промежутки возрастания функции: [-4.5; 1], промежутки убывания функции: [1; 5]
#3.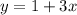 .
.
Это линейная функция, формула которой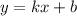 , где
, где
если k > 0, то функция возрастающая, если k < 0, то функция убывающая.
У нас k = 3, 3 > 0 => функция возрастающая.
#4. Найти область определения функции:
4.1
Область определения:
4.2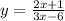
знаменатель не должен быть равным нулю: ,
, 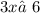 ,
, 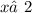
Область определения: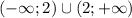
4.3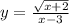
в числителе корень, число под корнем не должно быть отрицательным: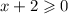 ,
, 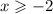
знаменатель не должен быть равным нулю: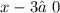 ,
, 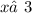
Область определения: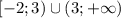
4.4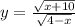
в числителе корень, число под корнем не должно быть отрицательным: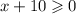 ,
, 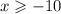
в знаменателе корень, число под корнем не должно быть отрицательным; знаменатель не должен быть равным нулю: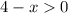 ,
, 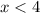
Область определения: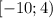
#5. Разложить на множители квадратный трёхчлен. Можно это сделать по формуле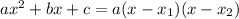 , где
, где 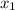 и
и 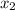 — корни уравнения
— корни уравнения 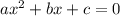 .
.
5.1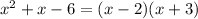
5.2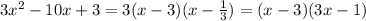
#6. Найти значение дроби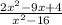 при
при  .
.
Для начала нужно упростить дробь.
Разложим квадратный трёхчлен из числителя на множители, по формуле из задания 5.
В знаменателе разность квадратов, используем формулу сокращенного умножения.
В итоге,
#7. а)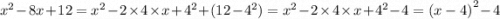
№5:
1) а) 24a + 56
б) -15a + 45
2) а) -43а + 8
б) -4p + 6
в) 1
г) 22у + 6
№7:
а) -2,31
б) -28,54
в) -3,36 - 8
г) -20,82 - 714,7
Объяснение:
№5:
1) а) 7 (5a + 8) - 11а
35а + 56 - 11а
24а + 56
б) 9x + 3 (15 - 8x)
9x + 45 - 24x
-15а + 45
2) а) 13а - 8 (7а - 1)
13а - 56а + 8
-43а + 8
б) -2 (2p - 1) + 4
-4p + 2 + 4
-4p + 6
в) 6 (с + 1) - 6с - 5
6с + 6 - 6с - 5
6 - 5
1
г) 19у + 2 (3 - 4у) + 11у
19у + 6 - 8у + 11у
22у + 6
№7:
а) 0,7b + 0,3 (b - 5) при b = -0,81
0,7b + 0,3b - 1,5
b - 1,5
-0,81 - 1,5
-2,31
б) 1,7 (a - 11) - 16,3 при а = 3,8
1,7a - 18,7 - 16,3
1,7 * 3,8 - 18,7 - 16,3
6,46 - 18,7 - 16,3
-28,54
в) 0,6 (4x - 14) - 0,4 (5x - 1) при x = 4 1/6
2,4x - 8,4 - 2x + 0,4
0,4x - 8,4 + 0,4
Рассмотрим 4 1/6 как 25/6 → 25,6
0,4 * 25,6 - 8,4 + 0,4
-3,36 - 8
г) 5 1/7 (y - 7) - 4 4/7 (14 - y) при у = - 0,3
Рассмотрим 5 1/7 как 36/7 → 36,7
Рассмотрим - 4 4/7 как 32/7 → 32,7
36,7 (y - 7) - 32,7 (14 - y)
36,7y - 256,9 - 457,8 + 32,7y
69,4y - 714,7
69,4 * (-0,3) - 714,7
-20,82 - 714,7