Реши неравенство −(6d+8)+(d−11)<0.
(В первое окошко запиши знак неравенства, во второе число; число запишите в виде десятичной дроби!)

В решении.

Объяснение:

Решите задачу с составления уравнения. Разность двух чисел равна 25, а разность их квадратов 875. Найдите эти числа​.

х - первое число.

у - второе число.

По условию задачи система уравнений:

х - у = 25

х² - у² = 875

Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:

х = 25 + у

(25 + у)² - у² = 875

625 + 50у + у² - у² = 875

50у = 875 - 625

50у = 250

у = 250/50

у = 5 - второе число.

х = 25 + у

х = 25 + 5

х = 30 - первое число.

Проверка:

30 - 5 = 25, верно.

30² - 5² = 900 - 25 = 875, верно.

См объяснение

Объяснение:

а) так как перед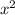 стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх

б) координаты вершины (x0, y0) вычисляются по формуле:

x0 =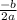 = = 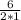3

y0 = y(x0) = 9 - 6*3 +5 = -4

Значит, координаты вершины : (3, -4)

c) Ось симметрии задается уравнением: x = 3

d) По теореме Виета:

Если x1, x2 - корни квадратного уравнения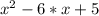 , ТО

Отсюда получаем корни x1 = 1; x2 = 5

Эти корни и есть нули функции

e) Дополнительные точки можно найти путем подстановки любых чисел: например, пусть x=0. тогда y = y(0) = 5

f) см прикрепленный рисунок