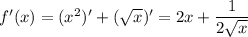Реши систему неравенств: {−3x>x−2(7x+1)16−x≥(1+7x)2−49x2 Выбери ответ системы неравенств:
x∈(−∞;1]
x∈(−0,2;+∞)
x∈(+∞;−∞)
x∈[−0,2;1)
x∈[−0,2;1]
x∈(−0,2;1]
x∈(−0,2;1)
Выбери целые ответы системы неравенств:
x=1
x∈∅
x=−1
x∈R
x=0
x=0,2
x=0,25
x=0,5
Реши неравенство 10−4t<5−6t.
ответ: t
(в одно окошко впиши знак неравенства, в другое — десятичную дробь).
Реши неравенство x+72>5−x3.
Выбери правильный вариант ответа:
x<-2,2
x>-2,2
x>-11
x>2,2
x<5
x>6
Число −13,4
решением неравенства |x|≥−13,4.
После деления обеих частей неравенства −2z≥12 на −2 получим (выбери подходящий ответ):
z≥−6
z≤6
z≤−6
z≥6
1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.
Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3
ответ: -3.
2. Производная функции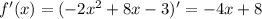
ответ: 16.
3.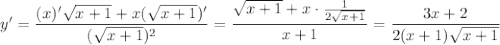
4. Производная функции: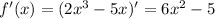
Используем геометрический смысл производной: f'(x₀) = tgα
ответ: 19.
5.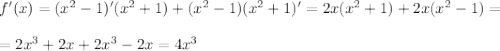
6.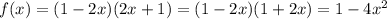
Производная функции: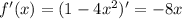 . Производная функции в точке 1, равна
. Производная функции в точке 1, равна 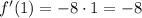
7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2
y(31) = 31/2 + 1/2 = 32/2 = 16
ответ: 16.
8.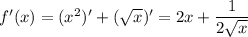
1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.
Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3
ответ: -3.
2. Производная функции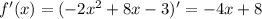
ответ: 16.
3.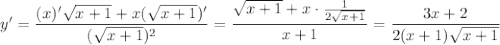
4. Производная функции: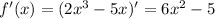
Используем геометрический смысл производной: f'(x₀) = tgα
ответ: 19.
5.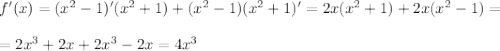
6.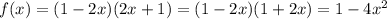
Производная функции: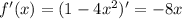 . Производная функции в точке 1, равна
. Производная функции в точке 1, равна 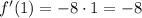
7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2
y(31) = 31/2 + 1/2 = 32/2 = 16
ответ: 16.
8.