Реши уравнение:

2x(x+20)2−x2(x+20)=0.

ответ:

x1=;x2=;x3=.

(Корни вводи в порядке возрастания их модулей.)

​

ответ:Здраствуйте!

Первый вариант:

Пусть первый работник может самостоятельно выполнить задание за х часов, а второй за (х+7) часов,зная, что вместе они могут выполнить задание за 12 часов, имеем уравнение: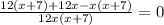

12x+84+12x-x²2-7x=0x²2-17x-84=0x1=21,  x2=-4 - не удовлетворяет условию задачиЗначит первый работникможет выполнить задание самостоятельно за 21 час, а второй - за 28 часовответ: 21 час и 28 часов

Второй вариант:

x - время работы первогох+7 - время работы второго1/х + 1/(х+7)= 1/1212(х+7)+12х=х(х+7)12x+84+12x=x^2+7xx^2-17x-84=0по теореме Виетаx1=21x2=-4 - отрицательным быть не может.х+7=28ответ -  21ч и 28ч

Объяснение:

Удачи)Хорошего настроения!

Відповідь:

1. А

2. A

Пояснення:

1. A парна ; Б не парна ; В ні парна ні не парна ; Г ні парна ні не парна

Функція є парною юякщо для будь-якого значення аргументу x вона задовольняє властивість f(-x) = f(x). Іншими словами, графік парної функції симетричний відносно вісі ординат.

Наприклад, функція f(x) = x^2 є парною, оскільки для будь-якого значення x виконується умова f(-x) = f(x). Також функція f(x) = cos(x) є парною, оскільки cos(-x) = cos(x).

Значення функції для аргументів x та -x в парних функціях збігаються, що відображає їх симетричність відносно вісі ординат.

2. Фото