Реши задачу:
Два кузнечика соревновались в прыжках. Известно, что каждый сделал несколько прыжков в одну сторону. Первый кузнечик первый раз прыгнул на 11м, а каждый следующий прыжок был в x раз больше предыдущего. Через три прыжка он оказался в y(м) от начала. Первый прыжок второго кузнечика был равен второму прыжку первого, а второй прыжок был в y раз больше первого прыжка. В результате, за два прыжка кузнечик оказался в 1616 метрах от начала. Найди x и y.
Объяснение:
1. Обозначим скорости велосипедиста и мотоциклиста х и у соответственно.
2. Расстояние межде городами,если ехать велосипедом - 7х,
а мотоциклом - 4у. ⇒ 7х=4у.
3. Скорость мотоциклиста больше скорости велосипедиста
на 18 км/ч. ⇒ у-х=18.
Получаем систему уравнений:
{7x=4y {7x=4*(x+18) {7x=4x+72 {3x=72 |÷3 {x=24
{y-x=18 {y=x+18 {y=42.
7х=4у=7*24=4*42=168.
ответ: скорость велосипедиста 24 км/ч,
скорость мотоциклиста 42 км/ч,
расстояние между городами 168 км.
Відповідь: ( -1; 5 ; 1 ; 3)
( або в порядку зростання: (-1; 1; 3; 5)
Пояснення:
(х²-4х)²-2(х²-4х)-15=0;
1. (вираз (х²-4х)- замінемо на одну букву наприклад р и це запишемо)
Нехай (х²-4х)=р, тоді
( підставимо р в рівняння)
р²-2р-15=0.
2. Знайдемо дискримінант
3.Знайдемо корні рівняння
р₁= (-b+D)/2a= (2+8)/2=10/2=5
р₂=(-b-D)/2a=(2-8)/2=-3
4) тепер підставляємо наше р₁ в рівняння (х²-4х)=р і рішаємо через дискримінант
(х²-4х)=5;
х²-4х-5=0
х₁=(-b-D)/2a=(4-6)/2=-1:
х₂=(-b+D)/2a=(4+6)/2=5;
5.тепер підставляємо наше р₂ в рівняння (х²-4х)=р і рішаємо через дискримінант
(х²-4х)=-3
х²-4х+3=0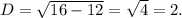
х₃=(-b-D)/2a=(4-2)/2=1:
х4=(-b+D)/2a=(4+2)/2=3;