решить: 1) 3sin ^2x + 4sinx cosx - 4 cos ^2x = 0
2) 5 \sin ^2 x + 2sin 2 x-cos^2x = 4
3)7 sin2x - 2sinx = 0

Показать ответ

Ответ:

syr00

14.04.2021 11:00

х автомашин требовалось сначала

12/х тонн груза планировалось перевозить на каждой машине

(х+2) автомашин фактически использовали

(12/(х+2) тонн груза фактически перевозила каждая машина

По условию

12/х > (12/(х+2) на 1

получаем уравнение:

$\frac{12}{x}-\frac{12}{x+2}=1$

$\frac{12}{x}-\frac{12}{x+2}-1=0$

$\frac{{12(x+2)-12x-x*(x+2)}}{x(x+2)}=0$

$\frac{{12x+24-12x-x^2-2x}}{x(x+2)}=0$

$\frac{{-x^2-2x+24}}{x(x+2)}=0$

ОДЗ:

-x^2-2x+24=0

x^2+2x-24=0

D=4-4*1*(-24)=4+96=100=10^2

$x_1=\frac{-2-10}{2}=-6$ не удовлетворяет ОДЗ

$x_2=\frac{-2+10}{2}=4$

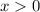
Получаем:

4 автомашины требовалось сначала

12/4 = 3 тонны груза планировалось перевозить на каждой машине

4+2 = 6 автомашин фактически использовали

ответ: 1) 4 автомашины требовалось сначала.

2) 6 автомашин фактически использовали.

3) 3 тонны груза планировалось перевозить на каждой машине.

0,0(0 оценок)

Ответ:

khokhr

16.09.2022 09:55

Первая парабола У=-Х²+4 имеет вершину на оси У (при Х=0 У=4) и ветви ее направлены вниз, т.к. перед Х² минус. Она симметрична оси У.

Вторая парабола У=(Х-2)² имеет вершину на оси Х (при Х=2 У=0) и ветви ее направлены вверх. Ее ось симметрии - прямая Х=2.

Чертим оси координат, отмечаем 0, точки с координатами (0;4) и (2;0), показываем ось симметрии Х=2.

Потом по клеточкам рисуем эти параболы (буквально по 2 пары точек) и видим, что пересечение двух парабол - именно в точках с координатами (0;4) и (2;0).

Общие точки на 2 параболах - при Х=0 и Х=2. Это и есть корни уравнения.

0,0(0 оценок)

Популярные вопросы: Алгебра