решить
2x -1 > 8
3x + 5 >14
9 - x> 1

16 - x > 0
2x - 9 > 5
x + 16 > 11

8 - 3x > 0
6 - x < 6
5x + 1 > 6

S = 5(15+2x)

Объяснение:

В решении задачи используем очень сложную формулу (шучу):

где U - скорость тела, S - расстояние, которое тело, T - время, за которое тело преодолело расстояние.

2 тела (автомобиля) выехали из одной точки в противоположные стороны.

Первый автомобиль преодолел за 5 часов S1=U1*t, или S1 =5x (потому что х - скорость первого автомобиля, а требуемое время - 5 часов (S1 - расстояние, которое преодолел первый автомобиль, а U1 - скорость первого автомобиля))

Второй автомобиль преодолел за 5 часов S2=U2*t, или S2 =5(x+15) (потому что скорость первого автомобиля на 15 больше первого, у первого - х, значит у второго - 15+х, а требуемое время - 5 часов (S2 - расстояние, которое преодолел второй автомобиль, а U2 - скорость второго автомобиля))

Складываем получившиеся выражения:

S = S1 + S2 = 5x + 5(x+15) = 5(x+15+x) = 5(15+2x)

ответ: Уравнение эллипса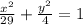 ; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)

Объяснение:

Дан эллипс: F₁ =(-5;0); F₂ =(5;0)  и B₁=(0;-2); B₂=(0;2). Напишите уравнение эллипса, найти оси и эксцентриситет

фокусное расстояние эллипса с = 5 (от точки F до точки О)

малая полуось b = 2

большая полуось а находится из соотношения

                             а² = b² + c²

                             a² = 2² + 5² = 4 + 25 = 29

уравнение эллипса:

- каноническое уравнение эллипса

Оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии.

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .

ε = с/ a = 5/√(29)