ответ: 8.
Решение: Подынтегральная функция на отрезке [0; 2] непрерывна, поэтому можно использовать классическую формулу Ньютона-Лейбница:
, где - первообразная функции .
ответ: 8.
Решение: Подынтегральная функция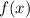
на отрезке [0; 2] непрерывна, поэтому можно использовать классическую формулу Ньютона-Лейбница: 