Обратим внимание, что выражения в скобках похожи. Обозначим выражение во второй скобке за t. Тогда получим t=x+1/x. Но вторую скобку заменить также "в лоб" мы не можем. Пойдём на небольшую хитрость. Возведём наше t в квадрат. Получим: t^2=x^2+2x*1/x+1/x^2=x^2+2+1/x^2. Получившееся значение уж больно похоже на то, что нам нужно. Всю картину портит только двойка справа. Но поскольку двойка балом не правит и никак не зависит от х, то просто перенесём её влево к нашему t^2. Тогда что мы имеем? А имеем мы вторую замену, поскольку только что выразили нашу первую скобку: x^2+1/x^2=t^2-2. Теперь собираем урожай и производим замену. Получаем: (t^2-2)+t=0 --> t^2+t-2=0. А это есть ни что иное как квадратное уравнение. Находим дискриминант: D=1-4*(-2)=1+8=9. И корни: t1= (-1+3)/2=1; t2=(-1-3)/2=-2 Делаем обратную замену. Вспомним, что наше t=x+1/x. Сначала подставим t1: x+1/x=1 | домножим на х x^2+1=x --> x^2-x+1=0. Получаем ещё одно квадратное уравнение, но уже относительно х. Находим его дискриминант: D=1-4<0. Дискриминант меньше нуля. Следовательно, корней нет. Теперь подставим t2: x+1/x=-2 |домножим на х x^2+1=-2x --> x^2+2x+1=0. Решим квадратное уравнение. Посчитаем дискриминант: D=4-4=0. Найдём корень уравнения. x=(-2+/-0)/2=-1 Теперь смотрим на наши квадратные уравнения относительно х (первое с t не трогаем). В первом квадратном уравнении у нас корней не было, во втором всего один. Он и является ответом ответ: х=-1
Но вторую скобку заменить также "в лоб" мы не можем. Пойдём на небольшую хитрость. Возведём наше t в квадрат. Получим: t^2=x^2+2x*1/x+1/x^2=x^2+2+1/x^2.
Получившееся значение уж больно похоже на то, что нам нужно. Всю картину портит только двойка справа. Но поскольку двойка балом не правит и никак не зависит от х, то просто перенесём её влево к нашему t^2.
Тогда что мы имеем? А имеем мы вторую замену, поскольку только что выразили нашу первую скобку: x^2+1/x^2=t^2-2.
Теперь собираем урожай и производим замену. Получаем:
(t^2-2)+t=0 --> t^2+t-2=0. А это есть ни что иное как квадратное уравнение.
Находим дискриминант: D=1-4*(-2)=1+8=9.
И корни: t1= (-1+3)/2=1;
t2=(-1-3)/2=-2
Делаем обратную замену. Вспомним, что наше t=x+1/x.
Сначала подставим t1:
x+1/x=1 | домножим на х
x^2+1=x --> x^2-x+1=0. Получаем ещё одно квадратное уравнение, но уже относительно х. Находим его дискриминант: D=1-4<0. Дискриминант меньше нуля. Следовательно, корней нет.
Теперь подставим t2:
x+1/x=-2 |домножим на х
x^2+1=-2x --> x^2+2x+1=0. Решим квадратное уравнение. Посчитаем дискриминант: D=4-4=0. Найдём корень уравнения. x=(-2+/-0)/2=-1
Теперь смотрим на наши квадратные уравнения относительно х (первое с t не трогаем).
В первом квадратном уравнении у нас корней не было, во втором всего один. Он и является ответом
ответ: х=-1
Не понял запись 2). б.
1). а). 16бу + 30 + 54у; б). -10х-8
2).а). -32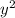
+ 56у +78; б). -
3). а). -35x-7bx-105b+2b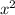
+ 4
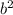x - 16
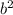; б). 2
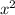+ 5х - 1
Объяснение:
1). а). 8*(бу + 3)*2 + 9*(3y - 1)*2
Умножаем (выделенные) числа:
16*(бу + 3) + 18*(3y - 1)
Распределяем 16 через скобки:
16*(бу + 3)
16бу + 16*3
16бу + 48
Распределяем 18 через скобки:
18*(3y - 1)
18*3y - 1*18
56у - 18
Вычисляем числа:
16бу + 48 + 56у - 18
16бу + 30 + 54у
б). (2x – 5)2 – 2(7x – 1)
Распределяем 2 через скобки:
(2x - 5)2
2х*2-5*2
4х-10
Распределяем -2 через скобки:
-2(7x - 1)
-2*7х-2*(-1)
-14х+2
Перевести подобные члены (х) и вычислить сумму:
4х-10-14х+2
-10х-8
2). а). (4у2 + 3) 2+(9 – 4у)2 –2(4y + 3) (4y – 9)
Вычислим произведение:
4у*2= 8у
Распределим обе 2 через скобки:
(8у + 3)*2
16у+6
(9 – 4у)*2
18-8у
Распределим -2 через скобки:
–2*(4y + 3)
(-8у-6)
Перемножим выражение в скобках:
(-8y +-6) * (4y – 9)
-8у*4у-8у*(-9)-6*4у-6*(-9)
-32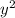
+ 72у - 24у + 54
Переводим подобные члены:
16у+6 + 18-8у -32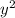
+ 72у - 24у + 54
56у+78-32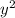
-32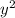
+ 56у +78
б). (а- баb + 9ь)(a2 + баb +9b2) - (а – 9ь)2
-
3). а). (х + 3b)(х – 35) - (х + 2b) (x — 2bx + 4b2)
Перемножить выражения в скобках и вычислить произведение:
(х + 3b)(х – 35)
х*х-35х+3bx-3b*35
-
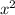35x+3bx-105b
4b*2 = 8b
Перемножить второе выражения в скобках:
-(х + 2b) (x — 2bx + 8b)
-(x*(x-2bx+8b)+2b*(x-2bx+8b))
-(
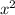- 2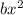
+ 8bx + 2bx - 4
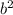x + 16
)
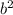Привести дробные числа и раскрыть скобки:
8bx + 2bx = 10bx
-
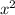* 35x+3bx-105b - 
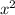+ 2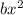
- 10bx + 4
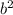x - 16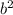
Сокращаем противоположные выраж-я и приводим подобные члены:
-35x-7bx-105b+2b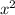
+ 4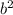
x - 16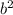
б). (х+1)(x2+x 1) - (x-1)(x2-x-1)
Изменяем порядок членов:
(х+1) * (2х+х) - (х-1) * (2х-х-1)
Приводим подобные числа:
(х+1) * 3х -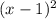
Распределим 3х через скобки:
(х+1) * 3х
х*3х+3х
Используем формулу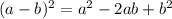
Изменяем знак каждого члена в скобках:
Приводим подобные числа:
2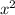
+ 5х - 1