Окончание одно числа в какой-то степени рано или поздно повторяются.
3¹ = 3
3² = 9
3³ = 27
3⁴ = 81
3⁵ = 243
3⁶ = 729
Как видно окончания уже повторяются, это кстати следует из последней цифры числа вот стало окончание 3, дальше точно будет 3·3=9 и потом 9·3=27 (7). Но почему же будет окончание 3 или другое повторяющееся в первый раз? Дело в том, что всего может быть 10 цифр в окончании и рано или поздно цифра повторится. Так вот.
3 в степени 1903, как мы выяснили у тройки окончание повторяются с периодом 4.
Окончание одно числа в какой-то степени рано или поздно повторяются.
3¹ = 3
3² = 9
3³ = 27
3⁴ = 81
3⁵ = 243
3⁶ = 729
Как видно окончания уже повторяются, это кстати следует из последней цифры числа вот стало окончание 3, дальше точно будет 3·3=9 и потом 9·3=27 (7). Но почему же будет окончание 3 или другое повторяющееся в первый раз? Дело в том, что всего может быть 10 цифр в окончании и рано или поздно цифра повторится. Так вот.
3 в степени 1903, как мы выяснили у тройки окончание повторяются с периодом 4.
_ - знак окончания в моём решении ;)
_3¹⁹⁰³ = _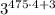
= _3³ = 7
ответ: 7.
Площадь прямоугольника S = a * b
Пусть x - одна из сторон площадки, тогда x+8 - другая сторона
x * (x+8) = 48
x² + 8x - 48 = 0
D = 8² - 4*1*(-48) = 64 + 192 = 256
x₁₂ = -8 ± √256 / 2*1
x₁ = -8 + 16 / 2 = 8 / 2 = 4
x₂ = -8 - 16 / 2 = - 24 / 2 = - 12 - не подходит под условие x≥0
Получается ответ системы x = 4(м) - одна из сторон площадки
4 + 8 = 12(м) - другая сторона
Для того, чтобы узнать сколько упаковок бордюра потребуется, нужно узнать периметр площадки P = 2 * (a+b)
P = 2 * (4+12) = 32 м
Получается, чтобы построить бордюр нужно 32 : 15 = 2,1(3)
Но если мы купим 2 упаковки, то нам не хватит бордюра на 2 метра. Получается, нам потребуется 3 упаковки материала.
ответ: Меньшая сторона детской площадки (целое число) равна:
4 м.
Большая сторона детской площадки (целое число) равна:
15 м.
Необходимое количество упаковок равно: 3