решить данные задания по математической статистике по теме «Характеристики НСВ решить данные задания по математической статистике по теме «Характеристики НСВ» ">

Рациональным числом называется такое число,которое не представляется в виде бесконечной периодической дроби.
А вот иррациональное - бесконечная периодическая дробь.
Иначе говоря,корень должен быть "тяжело извлекаем" в случае иррационального числа.
Вот,например случай 2)-рациональное,очевидно,это 13.
Рассмотрим случай 4).Переведём подкоренное в неправильную дробь - 25\4,корень извлекается,будет 5\2,следовательно,число рациональное.
В  случае 3) степень чётная,поэтому при перемножении можно убедиться,что число будет рациональным(целым здесь)
Из 1,6 корень не извлечём.
Хочется 4 приплести,да не выйдет.
Не так давно объясняла другому человеку случай 4).
Послушайте,если вам на экзамене попадутся десятичные дроби под корнями и потребуется выбрать рациональное число,берите ТО,У КОТОРОГО ПОСЛЕ ЗАПЯТОЙ ЧЁТНОЕ КОЛИЧЕСТВО ЗНАКОВ.
Здесь 1 запятая после запятой.Случай 1  вылетает.

Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.

1-ое свойство, которое понадобится

То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.

2-ое свойство, которое нам понадобится:

То есть довольно аналогичная вещь в произведении

На нашем примере все увидим

Находим остатки по модулю 31

Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,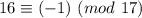 , но сейчас это не нужно), нам повезло, это 32

Учитываем, что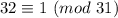 , получаем

То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым

Остаток 21, чудесно. Выполняем последний шаг.

То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.