данное дифференциальное уравнение является однородным.
Пусть , тогда , получаем
Это диф. уравнение с разделяющимися переменными.
Выполнив обратную замену, получаем общий интеграл
ответ: во вложении Объяснение:
данное дифференциальное уравнение является однородным.
Пусть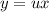 , тогда
, тогда 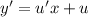 , получаем
, получаем
Это диф. уравнение с разделяющимися переменными.
Выполнив обратную замену, получаем общий интеграл
ответ: во вложении Объяснение: