Первое множество состоит из только тех , которые принадлежат ровно одному из множеств или . Поэтому всякий из этого множества принадлежит либо только (то есть множеству ), либо только (то есть множеству ). Следовательно, .
Второе множество состоит из тех , для которых либо , либо . Отсюда следует, что . Если при этом , то он не принадлежит ни одному из указанных множеств, противоречие, потому , значит, , откуда .
Первое множество состоит из только тех , которые принадлежат ровно одному из множеств
, которые принадлежат ровно одному из множеств 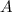 или
или 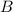 . Поэтому всякий
. Поэтому всякий  из этого множества принадлежит либо только
из этого множества принадлежит либо только 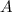 (то есть множеству
(то есть множеству 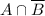 ), либо только
), либо только 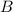 (то есть множеству
(то есть множеству 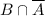 ). Следовательно,
). Следовательно, 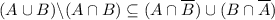 .
.
Второе множество состоит из тех , для которых либо
, для которых либо 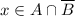 , либо
, либо 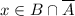 . Отсюда следует, что
. Отсюда следует, что 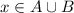 . Если при этом
. Если при этом 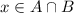 , то он не принадлежит ни одному из указанных множеств, противоречие, потому
, то он не принадлежит ни одному из указанных множеств, противоречие, потому 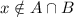 , значит,
, значит, 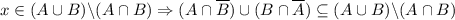 , откуда
, откуда 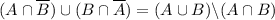 .
.