Геометрическая прогрессия — последовательность чисел b1, b2, b3,.. (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b1≠0 , q≠0.b1, b2=b1q, b3=b2q, ..., bn=bn-1q..., где
q знаменатель геометрической
прогрессии (шаг),
b1, b2, b3, ..., bn,.. - члены
геометрической прогрессии
3. n-й член геометрической прогрессии bn
определяется по формуле: bn=b1qn-1
4. Если
|q| < 1, — то прогрессия - бесконечная.
5. если последовательность является
бесконечно убывающей, то ее сумма
определяется по формуле: S∞ = b1 / (1-q)
в данном случае, b1=28, q=b2/b1=-14/28=-1/2,
|q|=|-1/2|=1/2<1—› значит, эта прогрессия бесконечная и S∞=b1/(1-q)=28/(1-(-1/2))=
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
18 2/3
Объяснение:
Вспомним:
Геометрическая прогрессия — последовательность чисел b1, b2, b3,.. (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b1≠0 , q≠0.b1, b2=b1q, b3=b2q, ..., bn=bn-1q..., гдеq знаменатель геометрической
прогрессии (шаг),
b1, b2, b3, ..., bn,.. - члены
геометрической прогрессии
3. n-й член геометрической прогрессии bn
определяется по формуле: bn=b1qn-1
4. Если
|q| < 1, — то прогрессия - бесконечная.5. если последовательность является
бесконечно убывающей, то ее сумма
определяется по формуле: S∞ = b1 / (1-q)
в данном случае, b1=28, q=b2/b1=-14/28=-1/2,
|q|=|-1/2|=1/2<1—› значит, эта прогрессия бесконечная и S∞=b1/(1-q)=28/(1-(-1/2))=
=28/(1+1/2)=28/(3/2)=28*2/3=56/3=18 2/3
Смотри решение.
Объяснение:
решения (через дискриминант):
Порядок решения:
а. Записываем уравнение в исходном виде;
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
решения (через теорему Виетта):
Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.
Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.
Общая формула квадратного уравнения: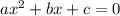
(для справок).
Теперь переходим к решению данного квадратного уравнения: