Если переменная х имеет только коэффициент (или даже не имеет его), но не возведена ни в какую степень и не поделена ни на какое число или переменную, то такая функция является линейной и графиком ее будет обычная прямая линия.
Для построения графика прямой линии принято использовать два , каждый из которых является правильным, точным и несложным.
Рассмотрим оба .
Первый состоит в том, что нужно найти точки пересечения функции с координатными осями. Таким образом, получим две точки, через которые проведем нужную прямую.
Найдем точки пересечения.
Точка пересечения с осью Ох находится методом решения уравнения, в котором переменная у равна нулю:
2x – 3 = 0
2х = 3
х = 3 / 2
х = 1,5.
Получена первая точка – (1,5; 0).
Точка пересечения с осью Оу находится методом подстановки вместо значения переменной х значения ноль:
у (0) = 2 * 0 – 3 = –3
Вторая точка – (0; –3).
Получены две точки, через которые проводится прямая.
Второй заключается в методе подстановки вместо переменной х любых двух значений и вычисления для них значений функции. Например, подставим вместо переменной х два значения – число 2 и число 4. Получим:
При х = 2 функция будет иметь значение:
у = 2 * 2 – 3 = 1 – первая точка (2; 1).
При х = 4 функция будет иметь значение:
у = 2 * 4 – 3 = 5 – вторая точка (4; 5).
И в первом, и во втором случае получим одинаковые прямые.
Если переменная х имеет только коэффициент (или даже не имеет его), но не возведена ни в какую степень и не поделена ни на какое число или переменную, то такая функция является линейной и графиком ее будет обычная прямая линия.
Для построения графика прямой линии принято использовать два , каждый из которых является правильным, точным и несложным.
Рассмотрим оба .
Первый состоит в том, что нужно найти точки пересечения функции с координатными осями. Таким образом, получим две точки, через которые проведем нужную прямую.
Найдем точки пересечения.
Точка пересечения с осью Ох находится методом решения уравнения, в котором переменная у равна нулю:
2x – 3 = 0
2х = 3
х = 3 / 2
х = 1,5.
Получена первая точка – (1,5; 0).
Точка пересечения с осью Оу находится методом подстановки вместо значения переменной х значения ноль:
у (0) = 2 * 0 – 3 = –3
Вторая точка – (0; –3).
Получены две точки, через которые проводится прямая.
Второй заключается в методе подстановки вместо переменной х любых двух значений и вычисления для них значений функции. Например, подставим вместо переменной х два значения – число 2 и число 4. Получим:
При х = 2 функция будет иметь значение:
у = 2 * 2 – 3 = 1 – первая точка (2; 1).
При х = 4 функция будет иметь значение:
у = 2 * 4 – 3 = 5 – вторая точка (4; 5).
И в первом, и во втором случае получим одинаковые прямые.
а) 2x^2-11x+12=0
2x^2-3x-8x+12=0
(2x-3)*(x-4)=0
2x-3=0 или x-4=0
2x=0+3 x=4
2x=3
x=3:2
x=1,5
б) 14x^2=9x
14x^2-9x=0
x(14x-9)=0
x=0 или 14x-9=0
x=9/14
в) 16x^2-49=0
16x^2=49
x^2=49:16
x^2=49/16
x=±7/4
г) x^2-36x+323=0
x(x-17)-19(x-17)=0
(x-17)(x-19)=0
x-17=0 или x-19=0
x=17 x=19
2.
p=46=2(a+b) все это делим на 2 чтобы от нее избавиться
23=a+b
b=23-a
s=120=ab
120=a(23-a)
120=23a-a^2
-a^2+23a-120=0
d=23^2-480=529-480=49
x1=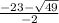 = -23-7/-2=-30/-2=15
= -23-7/-2=-30/-2=15
x2=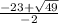 =-23+7/-2=-16/-2=8
=-23+7/-2=-16/-2=8
3.x^2+px=36=0 (a=1; b=p; c=36)
d=p^2-144
12=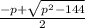
p=-15
x2=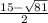 =15-9/2=6/2=3
=15-9/2=6/2=3