1) медіана = 1/2 гіпотенузи = 8,5см
гіпотенузa равна 8,5 · 2 = 17см
17см - гіпотенузa
2) першiй катет равен х см
Периметр прямокутного трикутника дорівнює 40 см.
40 - (17+х) = (23-х) - другий катет
3) По теореме Пифагора рiвняння:
х² + (23-х)² = 17²
х² + (529-2·23·х + х²) = 289
2х² - 46х + 529 = 289
2х² - 46х + 529 - 289 = 0
2х² - 46х + 240= 0
х² - 23х + 120 = 0
D = 23² - 4·1·120 = 529 - 480 = 49 = 7²
x₁ = = 8
x₂ = = 15
4) x₁ = 8см - першiй катет
23 - 8 = 15см - другий катет
x₂= 15см - першiй катет
23 - 15 = 8см - другий катет
Вiдповiдь: 8см; 15см
√f(x) ≥ g(x) ⇔ совокупности 2-х систем
1. f(x) ≥ 0
g(x) ≤ 0
2. g(x) > 0
f(x) ≥ g²(x)
√(10 - 7log(2) x + log²(2) x) ≥ 3 - log(2) x
одз x > 0 логарифм
(log(2) x - 2)(log(2) x - 5) > 0 корень
x ∈ (-∞,4] U [32, +∞)
общее x ∈ (0,4] U [32, +∞)
√((log(2) x - 2)(log(2) x - 5)) ≥ 3 - log(2) x
3 - log(2) x ≤ 0
(log(2) x - 2)(log(2) x - 5) ≥ 0
log(2) x = t
t ≥ 3
(t - 2)(t - 5) ≥ 0
[2] [5]
t ≤ 2
log(2) x ≤ 2
x ≤ 4
t ≥ 5
log(2) x ≥ 5
x ≥ 32
x ∈ [32, +∞)
3 - log(2) x > 0
x < 8
10 - 7log(2) x + log²(2) x ≥ (3 - log(2) x)²
10 - 7log(2) x + log²(2) x ≥ 9 - 6log(2) x + log²(2) x
1 ≥ log(2) x
x ≤ 2
учитывая одз
решение x ∈ (0,2] U [32, +∞)
не являются решением натуральные х ∈ (2, 32)
29 чисел от 3 до 31
1) медіана = 1/2 гіпотенузи = 8,5см
гіпотенузa равна 8,5 · 2 = 17см
17см - гіпотенузa
2) першiй катет равен х см
Периметр прямокутного трикутника дорівнює 40 см.
40 - (17+х) = (23-х) - другий катет
3) По теореме Пифагора рiвняння:
х² + (23-х)² = 17²
х² + (529-2·23·х + х²) = 289
2х² - 46х + 529 = 289
2х² - 46х + 529 - 289 = 0
2х² - 46х + 240= 0
х² - 23х + 120 = 0
D = 23² - 4·1·120 = 529 - 480 = 49 = 7²
x₁ =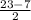 = 8
= 8
x₂ =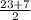 = 15
= 15
4) x₁ = 8см - першiй катет
23 - 8 = 15см - другий катет
x₂= 15см - першiй катет
23 - 15 = 8см - другий катет
Вiдповiдь: 8см; 15см
√f(x) ≥ g(x) ⇔ совокупности 2-х систем
1. f(x) ≥ 0
g(x) ≤ 0
2. g(x) > 0
f(x) ≥ g²(x)
√(10 - 7log(2) x + log²(2) x) ≥ 3 - log(2) x
одз x > 0 логарифм
(log(2) x - 2)(log(2) x - 5) > 0 корень
x ∈ (-∞,4] U [32, +∞)
общее x ∈ (0,4] U [32, +∞)
√((log(2) x - 2)(log(2) x - 5)) ≥ 3 - log(2) x
1. f(x) ≥ 0
g(x) ≤ 0
3 - log(2) x ≤ 0
(log(2) x - 2)(log(2) x - 5) ≥ 0
log(2) x = t
t ≥ 3
(t - 2)(t - 5) ≥ 0
[2] [5]
t ≤ 2
log(2) x ≤ 2
x ≤ 4
t ≥ 5
log(2) x ≥ 5
x ≥ 32
x ∈ [32, +∞)
2. g(x) > 0
f(x) ≥ g²(x)
3 - log(2) x > 0
x < 8
10 - 7log(2) x + log²(2) x ≥ (3 - log(2) x)²
10 - 7log(2) x + log²(2) x ≥ 9 - 6log(2) x + log²(2) x
1 ≥ log(2) x
x ≤ 2
учитывая одз
решение x ∈ (0,2] U [32, +∞)
не являются решением натуральные х ∈ (2, 32)
29 чисел от 3 до 31