Это второй замечательный предел:
Нужно только сделать некоторые преобразования:
Сделаем замену t=3x
Поскольку то и
Перепишем наш предел с учетом этой замены:
Поскольку известно что:
то
ответ:
Это второй замечательный предел:
Нужно только сделать некоторые преобразования:
Сделаем замену t=3x
Поскольку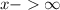 то и
то и 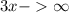
Перепишем наш предел с учетом этой замены:
Поскольку известно что:
то
ответ:![\lim_{x \to \infty} (1+\frac{1}{3x})^x=\sqrt[3]{e}](/tpl/images/0073/0415/45ad4.png)