Решить надо . два насоса работая совместно,могут осушить котлован за 20 часов. первый насос мог бы откочать из котлована воду на 9 часов быстрее чем второй насос.за сколько часов мог бы откочать воду из котлована каждый из насоса работая отдельно?
Обозначим всю работу по осушению котлован через 1. Пусть х ч и у ч требуется по одиночке на осушение котлована первому и второму насосам соответственно. Тогда производительность каждого насоса есть 1/х котлована за час и 1/у котлована за час соответственно. При разнице в 9 ч получим у-х=9, при одновременной работе получим (1/х + 1/у)*9 = 1.решаем систему уравнений
20(2x+9)=x(9+x)
40x+180=x^2+9x
x^2 -31x -180=0
х1=-5 не удовлетворяет условию
х2=36
Значит 36 ч требуется первому, а 36+9 = 45 ч -второму насосу.
Обозначим всю работу по осушению котлован через 1. Пусть х ч и у ч требуется по одиночке на осушение котлована первому и второму насосам соответственно. Тогда производительность каждого насоса есть 1/х котлована за час и 1/у котлована за час соответственно. При разнице в 9 ч получим у-х=9, при одновременной работе получим (1/х + 1/у)*9 = 1.решаем систему уравнений
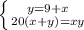
20(2x+9)=x(9+x)
40x+180=x^2+9x
x^2 -31x -180=0
х1=-5 не удовлетворяет условию
х2=36
Значит 36 ч требуется первому, а 36+9 = 45 ч -второму насосу.