Представим данное выражение в виде разложения на множители
где — неизвестный корень. Тогда
Приравниваем коэффициенты при степени x
Наибольшее значение из коэффициентов a и b: -2
ответ: -2.
Представим данное выражение в виде разложения на множители
где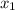 — неизвестный корень. Тогда
— неизвестный корень. Тогда
Приравниваем коэффициенты при степени x
Наибольшее значение из коэффициентов a и b: -2
ответ: -2.