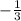- по определению.
Поскольку , то угол β находится в 3 четверти, в которой косинус отрицателен: .
Воспользовавшись основным тригонометрическим тождеством,
,
выражаем косинус: .
Так как , то
.
Тогда
ОТВЕТ:
Поскольку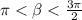 , то угол β находится в 3 четверти, в которой косинус отрицателен:
, то угол β находится в 3 четверти, в которой косинус отрицателен: 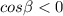 .
.
Воспользовавшись основным тригонометрическим тождеством,
выражаем косинус: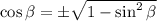 .
.
Так как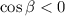 , то
, то
Тогда
ОТВЕТ: