Алгебра: Решить не равенство (5/x)+(-3/3-x) 0

Решить не равенство (5/x)+(-3/3-x)< 0

Показать ответ

Ответ:

ruchev06

25.02.2021 14:50

ответ:

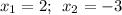
$x_1=2; \: \: x_2=-3$

Объяснение:

Построим в одной системе координат графики функций:

$y={x}^{2}$ (график - парабола) и y=-x+6 (график - прямая).

-------------------------------------------------------------------------------------------

Чтобы построить график функции, нужно дать аргументу несколько значений, от которых зависят значения функции .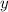

(таблицы с точками и графики функций смотрите ниже)

Графики пересекаются в точках с координатами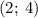 $(2; \: 4)$ и $(-3; \: 9)$ .

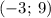Корнями уравнения служат абсциссы данных точек, то есть:

$x_1=2; \:\: x_2=-3$

-------------------------------------------------------------------------------------------

0,0(0 оценок)

Ответ:

plsplizovich

25.08.2021 03:11

Здесь вероятность будет равна отношению площади фигуры на которой расстояние от данной точки 1)превосходит 1, 2)не превосходит 1 к площади всего квадрата (геометрическая вероятность). Площадь квадрата со стороной 3:
$S_{\Omega}=3*3=9$
Теперь найдем интересующие нас фигуры:

В первом случае это квадрат со стороной 1, лежащий по центру нашего квадрата 3x3 (Действительно, расстояние от границы данной фигуры до границы квадрата 3x3 в точности равно 1, а потому для внутренних точек этого квадрата расстояние до сторон большого квадрата превосходит 1). (фигура 1)
Площадь этой фигуры:
S_1=1*1=1

Во втором случае это будет весь квадрат за исключением фигуры, описанной для первого случая (фигура 2)
Площадь этой фигуры:
S_2 = 3*3-1=8

А значит ответом будет:
1)
${S_1\over S_\Omega}={1\over 9}$

2)
${S_2\over S_\Omega}={8\over9}$

Фишку бросают наугад в квадрат со стороной 3, и она попадает в точку n. какова вероятность того, что