ОДЗ:
Также должно быть условие , но оно уже выполнено.
Знаменатель всегда положителен, значит нужно исследовать только числитель с учетом ОДЗ:
Выясним при каких значениях x числитель больше и меньше 0
Второе решение не имеет смысла, т.к. не лежит в нужной области раскрытия модуля
Таким образом, выяснили, что:
Возвращаясь к неравенству, имеем:
С учетом ОДЗ:
ответ:
ОДЗ:
Также должно быть условие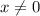 , но оно уже выполнено.
, но оно уже выполнено.
Знаменатель всегда положителен, значит нужно исследовать только числитель с учетом ОДЗ:
Выясним при каких значениях x числитель больше и меньше 0
Второе решение не имеет смысла, т.к. не лежит в нужной области раскрытия модуля
Таким образом, выяснили, что:
Возвращаясь к неравенству, имеем:
С учетом ОДЗ:
ответ:![x \in (1;2]](/tpl/images/1410/7302/f5865.png)