Кор(5-8х) + 2х <= 1 ОДЗ: х<= 5/8, 1-2x>=0, x<= 1/2
5 - 8x <= 1 - 4x + 4x^2
4x^2 + 4x - 4 >= 0
x^2 + x - 1 >= 0
x1 = (-1 - кор5)/2
х2 = (-1 + кор5)/2
(-беск; (-1 -кор5)/2]v[(-1+кор5)/2; беск)
Но с учетом ОДЗ только первая из приведенных областей
ответ:(-беск; (-1 -кор5)/2]
√(5-8х)≤1-2хПереходим к равносильной системе, состоящей из трех неравенств. Решаем каждое из них и, объединяя их решения, находим общее.1. 5-8х≥0-8х≥-5х≤5/8 2. 1-2х>0-2х>-1х<1/23. 5-8х≤(1-2х)²х²+х-1≥0х∈(-∞; ] U [ ; ∞)Объединяя, имеем такое общее решение: х∈(-∞; ]
Кор(5-8х) + 2х <= 1 ОДЗ: х<= 5/8, 1-2x>=0, x<= 1/2
5 - 8x <= 1 - 4x + 4x^2
4x^2 + 4x - 4 >= 0
x^2 + x - 1 >= 0
x1 = (-1 - кор5)/2
х2 = (-1 + кор5)/2
(-беск; (-1 -кор5)/2]v[(-1+кор5)/2; беск)
Но с учетом ОДЗ только первая из приведенных областей
ответ:(-беск; (-1 -кор5)/2]
√(5-8х)≤1-2х
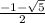 ] U [
] U [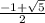 ; ∞)
; ∞)
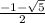 ]
]
Переходим к равносильной системе, состоящей из трех неравенств. Решаем каждое из них и, объединяя их решения, находим общее.
1. 5-8х≥0
-8х≥-5
х≤5/8
2. 1-2х>0
-2х>-1
х<1/2
3. 5-8х≤(1-2х)²
х²+х-1≥0
х∈(-∞;
Объединяя, имеем такое общее решение: х∈(-∞;