Корень квадратный не может быть отрицательным. Значит, чтобы неравенство выполнялось, нужно, чтобы выражение в скобках было меньше, либо равно нуля.
ОДЗ:
Решим неравенство графически: построим график функции и . Найдём те значения , при котором вторая функция больше либо равна первой.
Пересечение графиков функций в точке
Итак, функция больше либо равна функции на интервале
Объединим этот промежуток с ОДЗ и получим .
ответ:
Корень квадратный не может быть отрицательным. Значит, чтобы неравенство выполнялось, нужно, чтобы выражение в скобках было меньше, либо равно нуля.
ОДЗ: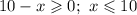
Решим неравенство графически: построим график функции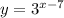 и
и 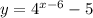 . Найдём те значения
. Найдём те значения  , при котором вторая функция больше либо равна первой.
, при котором вторая функция больше либо равна первой.
Пересечение графиков функций в точке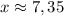
Итак, функция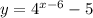 больше либо равна функции
больше либо равна функции 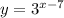 на интервале
на интервале 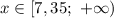
Объединим этот промежуток с ОДЗ и получим![x \in [7,35; \ 10]](/tpl/images/0203/6930/7972a.png) .
.
ответ:![x \in [7,35; \ 10]](/tpl/images/0203/6930/7972a.png)