Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
При х=0 функция имеет разрыв 1 рода .
При х=2 функция непрерывна.
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
На 1 рисунке нет чертежа функции при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
1.Упростите выражение 2с^2/c^-1 = 2с^(2-(-1))= 2с^3
2. Разложите на многочлены 5x^2-4x-1
Решим уравнение 5x^2-4x-1 = 0 по общей формуле Д= 16-4*5*9-1)=36
х1= (4+6)/10=1
х2=(4-6)/10= -2/10=-0,2
5x^2-4x-1 =5(х-1)(х+0,2)=(х-1)(х+1)
3.Решите уравнение x-5/2=x
Приведём к общему знаменателю и получим х-5=2х
х-2х=5
-х=5
х=-5
4. Решите неравенство 9x-2(3x-4)>2
9х-6х+12>2
3х+12>2
3х>2-12
3х>-10
х>-10 : 3
х> 3 целых 1/3
промежуток (-3 1/3; + бесконечность)
5) Всего по плану 100 % стульев
Фирма изготовила 85%. Найдём сколько процентов осталось изготовить
1) 100%-85%=15% - осталось
2) 45 *100 : 15 = 300 ст - всего по плану
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
При х=0 функция имеет разрыв 1 рода .
При х=2 функция непрерывна.
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
На 1 рисунке нет чертежа функции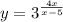
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .