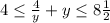Вот наступила золотая осеньe. самая красивая и живописная пора года. осень любит желтые, красные, оранжевые краски, а как любит она осыпать все золотом. вот приходишь в березовую рощу, и не можешь отвести глаз, все в золоте. на березках вместо листочков висят золотые монетки, и, кажется, что от одного дуновения ветерка они начнут тут же звенеть. золотом осыпает осень и парки, особенно липы. идешь и радуешься такой красоте. и начинаешь понимать, почему поэты так любили воспевать осень. а иногда просто слов нет, ну невозможно описать все ту красоту, которая открывается перед тобой. гуляешь по парку и не можешь нагуляться, так не хочется оставлять эту красоту. красиво рано утром, когда хорошая погода. золотые деревья просто сияют на фоне яркого голубого неба. нельзя не восхищаться природой, нет ничего прекраснее нее. ах! как здорово, просто дух захватывает от всего этого великолепия. золотая осень не уходи, порадуй нас еще немножко. но, к сожалению, это время короткое, и вот уже через неделю, деревья начинают сбрасывать свое убранство. а как не хочется расставаться со сказкой, как хочется еще полюбоваться живописными золотыми пейзажами.
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: .
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
1. -15 ≤ 1-2у ≤ 0
2.
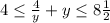
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2:
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 :
для у=8:
.
Т.е. имеем кривую с максимумами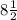
и минимумом 4.
Тогда