Решить по - с полным объяснением (можете кинуть на листочке решение) график функции у = √х проходит через точку а с ординатой 4. найдите абсциссу точки а. запишите наибольшее из чисел 3√7, 6√2, 2√14, √58.
Пусть х - цифра десятков, а у - цифра единиц первого двузначного числа, тогда первое число равно сумме (10х+у), а второе равно (10у+х). Известно, что первое число в 1,75 раз больше второго, поэтому 10х+у=1,75(10у+х) Также известно, что произведение первого числа на цифру его десятков в 3,5 раза больше второго числа, поэтому х(10х+у)=3,5(10у+х). Решаем систему: разделим второе уравнение на первое: Подставим найденное х=2 в какое-нибудь уравнение и найдем у: 20+у=1,75(10у+2) 20+у=17,5у+3,5 16,5у=16,5 у=1 Значит, 21 и 12 - искомые числа. ответ: 21 и 12.
Объяснение: 1) f(x) = ax² + bx + c. Определим коэффициенты а, b и с следующим образом.
Так как функция пересекает ось ОХ в точках 1 и -9, х = 1 и х = -9 - корни уравнения ax² + bx + c = 0, а значит нашу функцию можна разложить на линейные множители, используя формулу ax² + bx + c = a(x - x₁)(x - x₂), где х₁ и х₂ - корни уравнения.
т.е. f(x) = a(x - 1)(x + 9).
Найдем координату вершины параболы по оси ОХ. Так как вершина равноудалена от любых двух точек, имеющих одинаковую ординату, то можем найти ее как среднее арифметическое нулей функции f(x):
Вспомним, что экстремум (координата вершины по оси ОУ) равен -25. С другой стороны можем найти его, подставив вместо х найденное значение х₀: y₀ = f(х₀). Подсставляем: -25 = a(-4 - 1)(-4 + 9);
-25 = a · (-5) · 5; -25 = -25a ⇒ a = 1.
т.е. f(x) = (x - 1)(x + 9) = x² + 8x - 9. График - во вложении 1.
2. График - во вложении 2.
А) Функция - возрастающая, поэтому наименьшее ее значение достигается в наименьшей точке, принадлежащей отрезку - х = 3. Наименьшее значение функции на заданном отрезке - . Соответсвенно наибольшее значение функции на заданном отрезке достигается при х = 8, т.е оно равно .
Б) Найдем абсциссы точек пересечения графиков функций y = 2√x и x - y = 0 (y = x) - это решения уравнения 2√x = x.
С учетом ОДЗ - x ≥ 0 - обе части возведем в квадрат: (2√x)² = x², 4x = x², x² - 4x = 0, x(x - 4) = 0, откуда х = 0 или х = 4.
Ординаты аналогичны, так как мы имели дело с дополнительным условием у = х в виде второй функции. Искомые точки пересечения - (0; 0) и (4; 4) (для наглядности изображены на графике).
Известно, что первое число в 1,75 раз больше второго, поэтому
10х+у=1,75(10у+х)
Также известно, что произведение первого числа на цифру его десятков в 3,5 раза больше второго числа, поэтому х(10х+у)=3,5(10у+х).
Решаем систему:
разделим второе уравнение на первое:
Подставим найденное х=2 в какое-нибудь уравнение и найдем у:
20+у=1,75(10у+2)
20+у=17,5у+3,5
16,5у=16,5
у=1
Значит, 21 и 12 - искомые числа.
ответ: 21 и 12.
Объяснение:
Объяснение: 1) f(x) = ax² + bx + c. Определим коэффициенты а, b и с следующим образом.
Так как функция пересекает ось ОХ в точках 1 и -9, х = 1 и х = -9 - корни уравнения ax² + bx + c = 0, а значит нашу функцию можна разложить на линейные множители, используя формулу ax² + bx + c = a(x - x₁)(x - x₂), где х₁ и х₂ - корни уравнения.
т.е. f(x) = a(x - 1)(x + 9).
Найдем координату вершины параболы по оси ОХ. Так как вершина равноудалена от любых двух точек, имеющих одинаковую ординату, то можем найти ее как среднее арифметическое нулей функции f(x):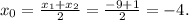
Вспомним, что экстремум (координата вершины по оси ОУ) равен -25. С другой стороны можем найти его, подставив вместо х найденное значение х₀: y₀ = f(х₀). Подсставляем: -25 = a(-4 - 1)(-4 + 9);
-25 = a · (-5) · 5; -25 = -25a ⇒ a = 1.
т.е. f(x) = (x - 1)(x + 9) = x² + 8x - 9. График - во вложении 1.
2. График - во вложении 2.
А) Функция - возрастающая, поэтому наименьшее ее значение достигается в наименьшей точке, принадлежащей отрезку - х = 3. Наименьшее значение функции на заданном отрезке -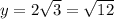 . Соответсвенно наибольшее значение функции на заданном отрезке достигается при х = 8, т.е оно равно
. Соответсвенно наибольшее значение функции на заданном отрезке достигается при х = 8, т.е оно равно 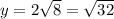 .
.
Б) Найдем абсциссы точек пересечения графиков функций y = 2√x и x - y = 0 (y = x) - это решения уравнения 2√x = x.
С учетом ОДЗ - x ≥ 0 - обе части возведем в квадрат: (2√x)² = x², 4x = x², x² - 4x = 0, x(x - 4) = 0, откуда х = 0 или х = 4.
Ординаты аналогичны, так как мы имели дело с дополнительным условием у = х в виде второй функции. Искомые точки пересечения - (0; 0) и (4; 4) (для наглядности изображены на графике).