прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: ).
Пусть , тогда:
Тогда:
1).
(теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить и после этого осталась чистая степень - 3)
(таким числом под логарифмом будет 27: )
(одинаковые логарифмы с основанием 3>1 - можем их убрать)
2).
(сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить и после этого осталась чистая степень - 1))
(таким числом под логарифмом будет 3: )
(одинаковые логарифмы с основанием 3>1 - можем их убрать)
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: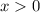
).
Пусть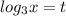
, тогда:
Тогда:
1).
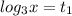
(таким числом под логарифмом будет 27: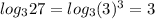
)
2).
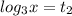
(таким числом под логарифмом будет 3: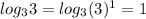
)
ответ: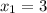
, 
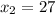
если я правильно рассуждаю, то это уравнение должно решаться так:
сначала раскрываем модуль:
1) 5х-3>0
5x>3
x>3/5
получаем уравнение:
5х-3+7=а
5х+4=а
2) 5х-3<0
5x<3
x<3/5
получаем уравнение:
3-5х+7=а
-5х+10=а
3) 1й случай
пусть прямая 5х+4=а парал-на прямой -5х+10=а, то их коэффициенты будут равны, то есть:
5х+4=а -5х+10=а
х=1 х=-1
5+4=а 5+10=а
а=9 а=15
2й случай
пусть первая прямая пересекает вторую в точке М. то первый коэффициент не равен второму. то есть:
а принадлежит от минус бесконечности до 9; от 9 до 15; от 15 до плюс бесконечности
может так?