Алгебра: решить пример по алгебре

решить пример по алгебре

Показать ответ

Ответ:

Баэхич

08.04.2020 16:30

Координаты точки пересечения прямых (2; 1)

Решение системы уравнений (2; 1)

Объяснение:

Определить коэффициент а и найти решение системы уравнений графически:

ax + 3y = 11

5x +2y = 12, если известно что первое уравнение этой системы обращается в верное равенство при x=8 и y= -7.

1) Вычисляем а. Для этого в первое уравнение подставляем заданные значения х и у:

ax + 3y = 11

а*8+3*(-7)=11

8а-21=11

8а=11+21

8а=32

а=4

Решим графически систему уравнений:

4x + 3y = 11

5x +2y = 12

Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.

Прежде преобразуем уравнения в более удобный для вычислений вид:

4x + 3y = 11 5x +2y = 12

3у=11-4х 2у=12-5х

у=(11-4х)/3 у=(12-5х)/2

Таблицы:

х -1 2 5 х -2 0 2

у 5 1 -3 у 11 6 1

Согласно графика, координаты точки пересечения прямых (2; 1)

Решение системы уравнений (2; 1)

0,0(0 оценок)

Ответ:

katysha087

27.02.2020 06:03

(x-a)(4x-1)(x+b)0

Нули выражения, записанного слева: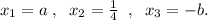 $x_1=a\; ,\; \; x_2=\frac{1}{4}\; \; ,\; \; x_3=-b .$

Решение неравенства имеет вид: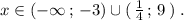 $x\in (-\infty \, ;\, -3)\cup (\, \frac{1}{4}\, ;\, 9\, )\; .$

Знаки выражения, записанного слева, чередуются таким образом;

$+++(-3)---(\frac{1}{4})+++(9)---$

Поэтому в условии надо перед всей левой частью поставить знак минус, или записать неравенство со знаком меньше, а не больше.

То есть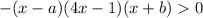 -(x-a)(4x-1)(x+b)0 или .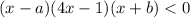

Тогда возможен вариант ответа: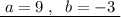 $\underline {\; a=9\; ,\; \; b=-3\; }$ .

Вид неравенства: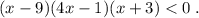 (x-9)(4x-1)(x+3)

Либо неравенство можно было записать , например, так:

$(9-x)(4x-1)(x+3)0\;$ или так $(x-9)(1-4x)(x+3)0\; .$

Но заданное неравенство не будет иметь тот ответ, что записан в условии . Наверное, произошла описка и неравенство было задано со знаком меньше, а не больше.

0,0(0 оценок)

Популярные вопросы: Алгебра