Войти Регистрация Спроси ai-bota

Решить пример sin(x/4)=sin^2(x/16)-cos^2(x/16)

Показать ответ

Ответ:

Princessa607

11.08.2020 08:18

$\sin\frac{x}{4}=-(\cos^2\frac{x}{16}-\sin^2\frac{x}{16})$

В левой части уравнения видим, что это формула косинуса двойного угла

$\sin\frac{x}{4}=-\cos(2\cdot\frac{x}{16})\\ \sin\frac{x}{4}=-\cos\frac{x}{8}$

Представим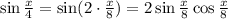 $\sin\frac{x}{4}=\sin(2\cdot\frac{x}{8})=2\sin\frac{x}{8}\cos\frac{x}{8}$ - синус двойного угла, получим

$2\sin\frac{x}{8}\cos\frac{x}{8}=-\cos\frac{x}{8}\\ 2\sin\frac{x}{8}\cos\frac{x}{8}+\cos\frac{x}{8}=0\\ \cos\frac{x}{8}(2\sin\frac{x}{8}+1)=0$

Произведение равно нулю, если хотя бы один из множителей равен нулю

$\cos\frac{x}{8}=0\\ \frac{x}{8}=\frac{\pi}{2}+\pi n,n \in \mathbb{Z}~~~|\cdot 8~~~~\Rightarrow~~~ \boxed{x=4\pi+8\pi n,n \in \mathbb{Z}}$

$2\sin \frac{x}{8}+1=0\\ \sin\frac{x}{8}=-0.5\\ \frac{x}{8}=(-1)^{k+1}\cdot\frac{\pi}{6}+\pi k,k \in \mathbb{Z}~~~\Rightarrow~~~ \boxed{x=(-1)^{k+1}\cdot\frac{4\pi}{3}+8\pi k,k \in \mathbb{Z}}$

0,0(0 оценок)

Популярные вопросы: Алгебра

bondaryulia2000

08.01.2022 06:22

Неравенство (x-a)(3x-1)(x+b) 0 имеет решение (-∞;-6)(;7). Найдите значения a и b....

SharkiLoge

19.05.2021 04:12

На каждой из трёх карточек написано одно из чисел: 1, 2, 3. какова вероятность того, что перевернув и перемешав их, вы первой возьмёте карточку с числом 1, а второй...

STPcopy

17.12.2020 02:17

с 30 ! при каком значении x значения выражений 2x+1, x+2 и 8−x будут последовательными членами прогрессии? найдите члены этой прогрессии....

seniorkovalyov

17.12.2020 02:17

Решить уравнения: 1)cos^{3}x sinx - sin^{3}x cosx=1/4; 2) 2cos^{2}2x+3sin4x+4sin^{2}2x=0; 3) sin(2x+12\pi/7) = 2sin(x-\pi /7)...

perrrii

24.03.2021 12:04

На некотором предприятии 95% продукции считается качественной. из качественных изделий 75% составляют изделия первого сорта, остальные – второго. какова вероятность...

aysemustafazade

08.07.2020 20:56

НАЙДИТЕ НУЛИ ФУНКЦИИ И ОБЛАСТЬ ОПРЕДЕЛЕНИЯ! НАПИШИТЕ ПОДРОБНО ОТ...

даладно30раз

30.03.2023 14:33

1. Дана функция y=6+b. При каких значениях b значение функции равно −10? 2. График функции y=5x−8 пересекает ось Oy в точке с координатами: ( ; ). 3. Найди координаты...

Денис56545

13.08.2022 17:25

Решите уровнение: а) (3x-2)²-(3x-4)*(4+3x)=0 ; б) 25y²-64=0...

ellia2

27.03.2021 14:44

4. Група з 18 учнів має такі оцінки з історії за семестр :8; 9:11; 10; 12:9:9:9; 10; 10; 8; 9; 10; 11; 8; 12;7, 11 Визначте середнє значення , моду та медіанувибірки...

лена6ада

23.08.2022 08:57

Найдите решение неравенства: [tex] \sin(2x) \cos(2x) \leqslant \frac{1}{4} [/tex] ...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку