(x-1)(x+5)>0 Находим точки, в которых неравенство равно нулю: x-1=0 x=1 x+5=0 x=-5 Наносим на прямую (-∞;+∞) эти точки: -∞-51+∞ Получаем три диапазона: (-∞;-5) (-5;1) (1;+∞) Для того, чтобы определить знак диапазона достаточно подставить хотя бы одно число из этого диапазона: (-∞;-5) Например, подставим число -7: (-7-1)(-7+5)=-8*(-2)=16>0 ⇒ + (-5;1) Подставим число этого диапазона 0: (0-1)(0+5)=-1*5=-5<0 ⇒ - (1;+∞) Подставим 2: (2-1)(2+5)=1*7=7>0 ⇒ + -∞+-5-1++∞ ⇒ x∈(-∞;-5)U(1;+∞).
Находим точки, в которых неравенство равно нулю:
x-1=0 x=1
x+5=0 x=-5
Наносим на прямую (-∞;+∞) эти точки:
-∞-51+∞
Получаем три диапазона: (-∞;-5) (-5;1) (1;+∞)
Для того, чтобы определить знак диапазона достаточно подставить хотя бы одно число из этого диапазона:
(-∞;-5) Например, подставим число -7: (-7-1)(-7+5)=-8*(-2)=16>0 ⇒ +
(-5;1) Подставим число этого диапазона 0: (0-1)(0+5)=-1*5=-5<0 ⇒ -
(1;+∞) Подставим 2: (2-1)(2+5)=1*7=7>0 ⇒ +
-∞+-5-1++∞ ⇒
x∈(-∞;-5)U(1;+∞).
сверху первый. В примере а) 2 корня. (я расписала подробно, но ты можешь решить так как я решила пример в б)
Б) D= 1^2-4*2*5
D=-39
корней нет.
2. а) D=(-11)^2-4*1*(-42) = 289 =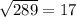
б) решу методом замены переменной:
y^2-13y+36=0
D=(-13)^2-4*36=25=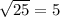
x^2=9 x^2=4
в) D=5^2-4*2*2 = 25-16 = 9 =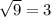
3. Длина первого катета - х см, тогда длина второго катета
будет (х + 5) см.
Площадь прямоугольного треугольника вычисляется по формуле:
S =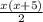
x*(x + 5) = 42*2
x² + 5x - 84 = 0
D = 25 + 4*1*84 = 361 =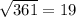
x₁ = (- 5 - 19)/2
x₁ = - 24/2 = - 12 посторонний корень
x₂ = (- 5 + 19)/2
x₂ = 7
7 см - длина первого катета
1) 7 + 5 = 12 (см) - длина второго катета
ответ: 7 см, 12 см