Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
svetamax70
29.10.2022 03:53 •
Алгебра
Решить уравнение: 2cos^2x+sinx+1=0
Показать ответ
Ответ:
Poжok1
02.09.2020 07:18
.
Объяснение:
Пусть
Тогда уравнение принимает вид:
Условию
удовлетворяет t=-1.
0,0
(0 оценок)
Популярные вопросы: Алгебра
darasnezko297
17.08.2021 15:46
А) постройте график функции у = - 2х - 2. б) определите, проходит ли график функции через точку а(10; - 20)....
АльпакаКайа
27.04.2022 23:29
Решите систему . методом сложения. x-y=5 x+y=7...
Alinka2i3
27.04.2022 23:29
1а) 2sin в квадрате х - 1 = 0 б) sin2х + 3 в корне cos2х = 0 2. дано f(х)=2х/2+х - 3sinх. найти f (о) 3. а) 2cosх - 2 в корне 0 б) 2х - х в квадрате/ х-4 0...
ovlvlk
27.04.2022 23:29
Решить систему уравнений удобным...
Каринакарина111
27.04.2022 23:29
Если что выражение под корнем всё до знака равно. перед корнем маленькая тройка. тут еле видно, но всё же. 1) ∛3×+116 = 5...
chechia
27.04.2022 23:29
Решите систему уравнений : г)(5х+6у=13 (7х+18у+1=0 б)(2х+3у+4=0 д)(7х+6у=1,5 (5х+6у=7 (4x-9y-5=0 е) (3х+4у=3,5 (-3x-4y=40...
girldasha1
27.04.2022 23:29
Решить систему уравнений! 2x+3y=5 3x-y=2 решите )...
karipzhanovalibek11
27.04.2022 23:29
Много пож- исследуйте функцию и посторойте ее график f(x)= -x3+2x2 1)найдите наибольшее и наименьшее значение а)f(x)= x4/2-2x3+2x2 на отрезке [-1; 2] б)f(x)=2cos2x-cos4x...
Надежда2709
30.03.2020 23:46
Егер m+1/m= 4/7 болса, онда өрнегі m^2+1/m^2 нешеге тең...
снегурочка01
16.07.2020 11:18
Сағат 1 сағ 30 минутты көрсетіп тұр. минут жəне сағат тілдерінің арасындағы бұрышты табыңыз....
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Объяснение:
Пусть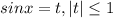 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
Условию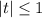 удовлетворяет t=-1.
удовлетворяет t=-1.