Область значений функции это , поскольку функция является возрастающей, как сумма двух возрастающих функций и минимум функции будет в точке x = 3.
- парабола, ветви которой направлены вниз. Найдем координаты вершины параболы
Поскольку на промежутке x ∈ [-3;+∞) функция убывает и на промежутке x ∈ [√3;+∞) функция возрастает. Значит, уравнение f(x)=g(x) имеет не более одного корня. х = 4 - корень уравнения
Область значений функции это
это 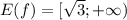 , поскольку функция является возрастающей, как сумма двух возрастающих функций и минимум функции будет в точке x = 3.
, поскольку функция является возрастающей, как сумма двух возрастающих функций и минимум функции будет в точке x = 3.
Поскольку на промежутке x ∈ [-3;+∞) функция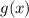 убывает и на промежутке x ∈ [√3;+∞) функция
убывает и на промежутке x ∈ [√3;+∞) функция 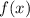 возрастает. Значит, уравнение f(x)=g(x) имеет не более одного корня. х = 4 - корень уравнения
возрастает. Значит, уравнение f(x)=g(x) имеет не более одного корня. х = 4 - корень уравнения
ответ: х = 4.