; Воспользуемся формулой разности квадратов:
;
; Отсюда получаем первый корень - x=3;
Думаю, что в уравнении ошибка, т.к. имеется еще один корень - корень уравнения ; Для полноты напишу его (можно использовать формулу Кардано):
Думаю, что в уравнении ошибка, т.к. имеется еще один корень - корень уравнения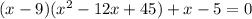 ; Для полноты напишу его (можно использовать формулу Кардано):
; Для полноты напишу его (можно использовать формулу Кардано):