1)
cos2x = 0
x = pi/4 + pik/2, k: Z.
2) Поделив на cosx:
tgx = 1
x = pi/4 + pik, k: Z.
3) Воспользуемся формулой приведения:
cos(pi/2 -x) - cos3x = 0
2sin(pi/4 +x)sin(2x-pi/4) = 0
sin(pi/4 +x) = 0 sin(2x-pi/4) = 0
x = -pi/4 + pi*k x = pi/8 + pi*k/2, k: Z
4) sinx - cosx = -1
1)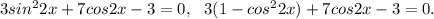
cos2x = 0
x = pi/4 + pik/2, k: Z.
2) Поделив на cosx:
tgx = 1
x = pi/4 + pik, k: Z.
3) Воспользуемся формулой приведения:
cos(pi/2 -x) - cos3x = 0
2sin(pi/4 +x)sin(2x-pi/4) = 0
sin(pi/4 +x) = 0 sin(2x-pi/4) = 0
x = -pi/4 + pi*k x = pi/8 + pi*k/2, k: Z
4) sinx - cosx = -1