1) - "Инструкция по построению графика своими руками";
2) - Сам график;
3). - Асимптоты.
_____________________________________
Асимптоты здесь - это вертикальная прямая, параллельная оси ординат и проходящая через точку (задается уравнением ) и наклонная, которая, как показывают вычисления, является графиком линейной функции .
Пересечения с осями координат происходят в точках и . Чтобы их найти, достаточно в уравнение, задающее функцию, поочередно подставить и .
Даны функции, сначала их нужно построить. 1) Чтобы построить функцию y=x^2 , рисуем таблицу, в которой подставляем небольшие иксы и находим игреки. И по получившимся точкам чертим параболу. 2) Чертим x=1 и x=2 . Это вертикальные прямые, которые пересекаются с осью х в точках (1;0) и (2;0) . 3) Чертим y=0 . Это горизонтальная линия, которая полностью совпадает с осью х. Начертили, теперь видно, какую фигуру ограничивают эти линии ( она закрашена красным) . Нужно найти ее площадь.
Площадь равна определенному интегралу той функции (x^2) . Пределы - это иксы, на которых заканчивается и начинается данная фигура. В данном случае это 2 и 1. (на графике обвела их красными кружочками). Вот и все, решаем интеграл.
1) - "Инструкция по построению графика своими руками";
2) - Сам график;
3). - Асимптоты.
_____________________________________
Асимптоты здесь - это вертикальная прямая, параллельная оси ординат и проходящая через точку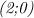
(задается уравнением 
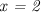) и наклонная, которая, как показывают вычисления, является графиком линейной функции 
.
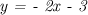Пересечения с осями координат происходят в точках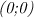
и 
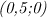. Чтобы их найти, достаточно в уравнение, задающее функцию, поочередно подставить 
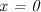и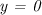 
.
А таблица точек - в прикрепленном файле.
Даны функции, сначала их нужно построить.
1) Чтобы построить функцию y=x^2 , рисуем таблицу, в которой подставляем небольшие иксы и находим игреки. И по получившимся точкам чертим параболу.
2) Чертим x=1 и x=2 . Это вертикальные прямые, которые пересекаются с осью х в точках (1;0) и (2;0) .
3) Чертим y=0 . Это горизонтальная линия, которая полностью совпадает с осью х.
Начертили, теперь видно, какую фигуру ограничивают эти линии ( она закрашена красным) . Нужно найти ее площадь.
Площадь равна определенному интегралу той функции (x^2) . Пределы - это иксы, на которых заканчивается и начинается данная фигура. В данном случае это 2 и 1. (на графике обвела их красными кружочками). Вот и все, решаем интеграл.