|x-1|>|x+2|-3 |x-1|-|x+2|>-3 Раскроем модули. Приравняем каждое подмодульное выражение к нулю и найдем точки,в которых подмодульные выражения меняют знак: x-1=0 x+2=0 x=1 x=-2 Нанесем эти значения Х на числовую прямую:
(-2)(1)
Мы получили три промежутка.Найдем знаки каждого подмодульного выражения на каждом промежутке:
(-2)(1) x-1 - - + x+2 - + +
Раскроем модули на каждом промежутке: 1)x<-2 На этом промежутке оба подмодульных выражения отрицательны,поэтому раскрываем модули с противоположным знаком: -x+1+x+2>-3 3>-3 - неравенство верное при любых Х на промежутке x<-2
2) -2<=x<1 На этом промежутке первое подмодульное выражение отрицательное(его мы раскроем с противоположным знаком),а второе - положительное, и его мы раскроем с тем же знаком: -x+1-x-2>-3 -2x-1>-3 -2x>1-3 -2x>-2 x<1 С учетом промежутка -2<=x<1 получаем x e [-2;1)
3)x>=1 На этом промежутке оба подмодульных выражения положительные, поэтому раскрываем их без смены знака: x-1-x-2>-3 -3>-3 Неравенство не имеет решений на этом промежутке Соединим решения 1 и 2 промежутков и получим такой ответ: x e(-беск.,1)
Если не учитывать, что 100% тоже больше 94%, то: Пусть х - число домов в этом районе, а х-1 - число домов, имеющих больше 5 этажей (чтобы найти минимально значение х, разница между числом домов, имеющих больше 5 этажей, и общим числом домов должна быть минимальна)
Получаем уравнение:
Проверка подбором
11 домов имеют больше 5 этажей 12 домов всего 11 / 12 = 0,91(6) = 91,(6)% Не подходит.
... 15 домов имеют больше 5 этажей 16 домов всего 15 / 16 = 0,9375 = 93,75% Не подходит.
16 домов имеют больше 5 этажей 17 домов всего 16 / 17 = 0,941176... = 94,1176...% Подходит.
ответ: 17 - наименьшее число домов в данном районе.
|x-1|-|x+2|>-3
Раскроем модули.
Приравняем каждое подмодульное выражение к нулю и найдем точки,в которых подмодульные выражения меняют знак:
x-1=0 x+2=0
x=1 x=-2
Нанесем эти значения Х на числовую прямую:
(-2)(1)
Мы получили три промежутка.Найдем знаки каждого подмодульного выражения на каждом промежутке:
(-2)(1)
x-1 - - +
x+2 - + +
Раскроем модули на каждом промежутке:
1)x<-2
На этом промежутке оба подмодульных выражения отрицательны,поэтому раскрываем модули с противоположным знаком:
-x+1+x+2>-3
3>-3 - неравенство верное при любых Х на промежутке x<-2
2) -2<=x<1
На этом промежутке первое подмодульное выражение отрицательное(его мы раскроем с противоположным знаком),а второе - положительное, и его мы раскроем с тем же знаком:
-x+1-x-2>-3
-2x-1>-3
-2x>1-3
-2x>-2
x<1
С учетом промежутка -2<=x<1 получаем x e [-2;1)
3)x>=1
На этом промежутке оба подмодульных выражения положительные, поэтому раскрываем их без смены знака:
x-1-x-2>-3
-3>-3
Неравенство не имеет решений на этом промежутке
Соединим решения 1 и 2 промежутков и получим такой ответ:
x e(-беск.,1)
Если не учитывать, что 100% тоже больше 94%, то:
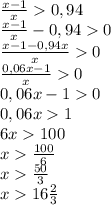
Пусть х - число домов в этом районе, а х-1 - число домов, имеющих больше 5 этажей
(чтобы найти минимально значение х, разница между числом домов, имеющих больше 5 этажей, и общим числом домов должна быть минимальна)
Получаем уравнение:
Проверка подбором
11 домов имеют больше 5 этажей
12 домов всего
11 / 12 = 0,91(6) = 91,(6)%
Не подходит.
...
15 домов имеют больше 5 этажей
16 домов всего
15 / 16 = 0,9375 = 93,75%
Не подходит.
16 домов имеют больше 5 этажей
17 домов всего
16 / 17 = 0,941176... = 94,1176...%
Подходит.
ответ: 17 - наименьшее число домов в данном районе.