решить задачки на вероятность

1. Относительная частота занятий, пропущенных студентом 0,04. Сколько было пропусков, если он присутствовал 168 раз?
2. Брошены две игральные кости, какова вероятность, что выпадет не более 5 очков?
3. В группе 12 студентов, 7 из них отличники. Случайным образом отобрано 5 студентов. Какова вероятность, что 3 из них будут отличники?
4. В группе 25 студентов. Для производственной практики предоставлено 10 мест в Берлин, 8 в Лондон, 7 в Париж. Какова вероятность, что три определенных студента попадут на практику в один город?
5. Сколько раз надо подбросить пару игральных костей, чтобы с вероятностью не менее чем 0,5 можно было утверждать, что хотя бы один раз появится 12 очков?
6. На одинаковых карточках написаны буквы А,В,Г,Л,О. Какова вероятность, что составится слово ВОЛГА, если карточки после перемешивания раскладывают в порядке поступления?
7. Электрические лампочки изготовляются на трех заводах. Первый производит 40% продукции, второй – 35%, а остальное третий. В продукции первого завода 75% стандартных лампочек. В продукции второго – 80%, в продукции третьего – 88%. Из общей продукции была взята лампочка, которая оказалась нестандартной. Какова вероятность, что она изготовлена на втором заводе?
8. 98% часов, изготавливаемых на заводе, соответствуют требованиям качества. 2% требуют дополнительной регулировки. 300 часов принято на реализацию. Если среди них окажется 11 или более часов требующих дополнительной регулировки, то партия товара возвращается заводу. Какова вероятность, что партия часов будет принята на реализацию?
9. Чему равна вероятность того, что среди 600 пар обуви поступивших в продажу окажутся высшего сорта от 228 до 252 пар? Известно, что в этой партии наудачу взятая пара обуви будет высшего сорта с вероятностью 0,4.
10. Вероятность обрыва нити на прядильном станке 0,001.Какова вероятность нить оборвется не более двух раз на 100 станках?

Показать ответ

Ответ:

cygrobik111

22.03.2023 11:59

-6,7059

Объяснение:

y=2x-ln(x+4)^2

Сначала находим производную нашей функции

$y'=2-\frac{1}{(x+4)^2}$

Затем приводим функцию к нулю, превратив его в уравнение

$2-\frac{1}{(x+4)^2} =0$

Область допустимых значений (ОДЗ) нашего уравнения ровна

$x+4\neq 0\\x\neq -4$

Упрощаем уравнение, домножив обе части на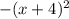 -(x+4)^2

Получаем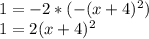 $1=-2*(-(x+4)^2)\\1=2(x+4)^2$

Упростим уравнение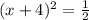 $(x+4)^2=\frac{1}{2}$

Возведем обе части под корень, чтоб избавиться от квадрата

$\left \{ {{x+4=\sqrt{\frac{1}{2} } } \atop {x+4=-\sqrt{\frac{1}{2} } }} \right.\\\left \{ {{x+4=\frac{\sqrt{2} }{2} } \atop {x+4=-\frac{\sqrt{2} }{2} }} \right. \\\left \{ {{x=\frac{\sqrt{2} }{2}-4 } \atop {x=-\frac{\sqrt{2} }{2}-4 }} \right. \\$

x≈ -3.29 и x≈-4.70

Делаем проверку ОДЗ

$-3.29\neq -4\\ -4.70\neq -4$

Оба выражения верны, следовательно чертим числовую прямую

\\\\\\\\\\\\\\\\\\\\\\\\\•\\\\\\\\\\\\•ххххххххх•ххххххх•////////////////////////////→

-4.70 -3.5 -3.29 0

Нам подходит только x≈-3.29

Теперь в саму функцию подставляем x

$y(\frac{\sqrt{2} }{2}-4)=2*( \frac{\sqrt{2} }{2}-4)-ln(\frac{\sqrt{2} }{2}-4)^2\\y(\frac{\sqrt{2} }{2}-4)=\sqrt{2} -8-\frac{ln(2)^2}{4} \\$

$y(\frac{\sqrt{2} }{2} -4)$ ≈ -6.7059

ответ: Наибольшее значение функции y=2x-ln(x+4)^2 на отрезке [-3,5;0] равно -6,7059

0,0(0 оценок)

Ответ:

Romanby1

12.11.2021 09:14

В решении.

Объяснение:

Сравнить выражения, если c > d:

а) 0,3с и 0,3d

На примере:

с=3, d=2 c > d

0,3 * 3 > 0,3 * 2

То есть, если множитель при с и d одинаковый, то произведение множителя на с будет больше произведения множителя на d, потому что с > d по условию (если множитель положительный).

0,3с > 0,3d

б) -0,5с и -0,5d

Здесь наоборот, так как числа в результате умножения отрицательные, то чем больше число по величине, тем оно меньше из-за того, что отрицательное.

На примере:

с=3, d=2 c > d

-0,5 * 3= -1,5

-0,5 * 2= - 1

-1,5 < - 1

В данном случае -0,5с < -0,5d

0,0(0 оценок)

Популярные вопросы: Алгебра