Пусть . Тогда левый логарифм положителен, а правый отрицателен. Если мы домножим обе части неравенства на произведение логарифмов, неравенство сменит знак:
Логарифм с основанием, большим единицы, — монотонно возрастающая функция, поэтому:
Методом интервалов получим, что . Объединяя с первым условием, получим: .
Пусть теперь . Тогда, когда мы умножим обе части неравенства на произведение логарифмов, неравенство сохранит знак:
Пусть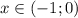 . Тогда левый логарифм положителен, а правый отрицателен. Если мы домножим обе части неравенства на произведение логарифмов, неравенство сменит знак:
. Тогда левый логарифм положителен, а правый отрицателен. Если мы домножим обе части неравенства на произведение логарифмов, неравенство сменит знак:
Логарифм с основанием, большим единицы, — монотонно возрастающая функция, поэтому:
Методом интервалов получим, что![x \in [-2;1]](/tpl/images/4978/0209/a3a78.png) . Объединяя с первым условием, получим:
. Объединяя с первым условием, получим: 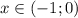 .
.
Пусть теперь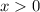 . Тогда, когда мы умножим обе части неравенства на произведение логарифмов, неравенство сохранит знак:
. Тогда, когда мы умножим обе части неравенства на произведение логарифмов, неравенство сохранит знак:
Проделываем всё то же самое:
Подходит только правый интервал:
ответ: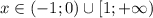
На скриншоте проверка на компьютере.
Если что-нибудь непонятно — спрашивай.