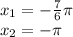Функция — соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Если концы ломаной совпадают, то такая ломаная называется замкнутой.
для простоты и наочности на примере рисунка из вложения :
пусть у нас есть замкнутая ламанаяА1А2А3А4А5
в нашем случае крайняя левая точка по оси Ох это А2, крайняя правая А5, путь от крайней левой до крайней правой точки можно осуществить двумя путями, в нашем случае либо (за часовой стрелкой) А2А1А5 либо (против часовой) А2А3А5
оба этих пути задают какието графики, но нельзя задать общим правилом функции ра на оба пути так как мы получим , что тогда между нашими крайними точками А2 и А5 для любого х будет как минимум по два значения , одно с "верхнего" пути ,второе с "нижнего", что противоречит определению функции.
Так что определение замкнутой ломаной входит в противоречие с определением для функции. Вывод - нельзя.
(замкнутая ломаная состоит минимум из трех вершин, и в ней в любом случае можно найти левую и правую крайнюю соотнося с осью координат, а вторая ось будет пересекать ломаную как минимум в двух точках между этими крайними)
Подставляем n = 0 - неравенство не выполнено. n = 1 - неравенство не выполнено. Следовательно, при n ≥ 0 решений не будет, т.к. (-1)^n + 6n - функция возрастающая.
Пусть n = -1, тогда выражение Так как 3.14 < π < 3.15, то
-22.05 < -7π < -21.98. Очевидно, оно попадает на промежуток (-24; -18). Значит, при n = -1 решение есть на данном отрезке. Подставим n = -1 в серию корней:
Такими же рассуждениями приходим к тому, что n ≤ -2 так же не являются решениями.
Теперь рассмотрим вторую серию корней:
Тут совсем все просто: при m = 0, очевидно, неравенство не выполнено. При m = 1 так же. Так как выражение при возрастании m увеличивается, то и m ≥ 2 также не подходят.
Пусть m = -1, тогда:
Очевидно, что это так. Подставляя m = -2 понимаем, что число меньше -4.
Нельзя
Объяснение:
Немного общих вводных:
Функция — соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Если концы ломаной совпадают, то такая ломаная называется замкнутой.
для простоты и наочности на примере рисунка из вложения :
пусть у нас есть замкнутая ламанаяА1А2А3А4А5
в нашем случае крайняя левая точка по оси Ох это А2, крайняя правая А5, путь от крайней левой до крайней правой точки можно осуществить двумя путями, в нашем случае либо (за часовой стрелкой) А2А1А5 либо (против часовой) А2А3А5
оба этих пути задают какието графики, но нельзя задать общим правилом функции ра на оба пути так как мы получим , что тогда между нашими крайними точками А2 и А5 для любого х будет как минимум по два значения , одно с "верхнего" пути ,второе с "нижнего", что противоречит определению функции.
Так что определение замкнутой ломаной входит в противоречие с определением для функции. Вывод - нельзя.
(замкнутая ломаная состоит минимум из трех вершин, и в ней в любом случае можно найти левую и правую крайнюю соотнося с осью координат, а вторая ось будет пересекать ломаную как минимум в двух точках между этими крайними)
Подставляем n = 0 - неравенство не выполнено. n = 1 - неравенство не выполнено. Следовательно, при n ≥ 0 решений не будет, т.к. (-1)^n + 6n - функция возрастающая.
Пусть n = -1, тогда выражение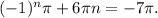 Так как 3.14 < π < 3.15, то
Так как 3.14 < π < 3.15, то
-22.05 < -7π < -21.98. Очевидно, оно попадает на промежуток (-24; -18). Значит, при n = -1 решение есть на данном отрезке. Подставим n = -1 в серию корней:
Такими же рассуждениями приходим к тому, что n ≤ -2 так же не являются решениями.
Теперь рассмотрим вторую серию корней:
Тут совсем все просто: при m = 0, очевидно, неравенство не выполнено. При m = 1 так же. Так как выражение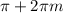 при возрастании m увеличивается, то и m ≥ 2 также не подходят.
при возрастании m увеличивается, то и m ≥ 2 также не подходят.
Пусть m = -1, тогда:
Очевидно, что это так. Подставляя m = -2 понимаем, что число меньше -4.
Вопросы ниже в комменты.
ответ: