решить задания. Геометрия 8 класс. Без корней желательно!

Показать ответ

Ответ:

Женя3725

23.06.2022 08:05

Прежде всего раз график f(х) касается прямой у=2х-16, то это означает, что у=2х-16 является касательной к f(x).

График функции f(x)=x²+px+q проходит через начало координат

отсюда получаем f(0)=0
или 0=0²+р*0+q
откуда q=0
значит график функции
f(x) имеет вид f(x)=x²+px

Найдем производную f(x)=x²+px
f'(x)=2x+p

Наименьшее значение f(x) будет достигаться в точке Хмин
при f'(Xмин)=0
2Хмин+р=0 откуда Хмин= - р/2 (#)
Нам остаётся найти p

Уравнение касательной к f(x) в точке Хо
у=f(Xo)+f'(Xo)(x-Xo)

f(X0)=Xo²+pXo
f'(Xo)=2Xo+p

значит
у= (Xo²+pXo)+
+(2Xo+p)(х-Хо)=
=(2Xo+p)х+
+(Xo+pXo-2Хо²-pXo)=
=(2Xo+p)х +(-Xo²)
Наша касательная по условию:
y=2х-16

откуда, приравнивая коэффициенты при x и свободные члены, получим :
2Хо+р=2 (1)
-Xo²=-16 и(2)

из (2) получаем Xo²=16 и (Хо)1,2=±4
из (1) находим p=2-2Xo
p1=2-2*4=-6
f1(x)=x²-6x (синий график , см фото)
p2=2+2*4=10
f2(x)=x²+10x (черный график, см фото)
касательная у=2х-16 обозначена красным цветом

из (#)
Хмин= - р/2
подставляем найденные значения p в эту формулу:
(Xmin)1= -(-6)/2=3
(Xmin)2= -10/2=-5

Наименьшие значения функций:
f((Xmin)1)= 3²-6*3=-9
f((Xmin)2)=(-5)²+10(-5)=-25
(два решения)
30 , тема: уравнение касательной к графику объяснить досконально, непонятна тема график функции f(x)

30 , тема: уравнение касательной к графику объяснить досконально, непонятна тема график функции f(x)

0,0(0 оценок)

Ответ:

sasha228111228

04.03.2020 00:22

1) Возьмём числитель первой дроби за X. Тогда знаменатель будет равен X+3. Первая дробь будет равна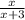 $\frac{x}{x+3}$ Если увеличить числитель первой дроби на два и знаменатель на четыре, то вторая дробь будет равна 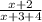$\frac{x+2}{x+3+4}$ В условии задания сказано, что вторая дробь больше первой на 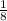$\frac{1}{8}$ , значит разность второй и первой дроби будет равна одной восьмой. Составим уравнение.

$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$ Чтобы избавиться от дробей умножаем каждое число на (x+7)·(x+3)·8

(x+2)·(x+3)·8 - x·(x+7)·8=(x+7)·(x+3)

(x²+3x+2x+6)·8 - (x²+7x)·8=(x+7)·(x+3)

8x²+24x+16x+48-8x²-56x=x²+3x+7x+21 Переносим всё в левую сторону и приравниваем выражение к нулю. Упростив, получим:

-x²-26+27=0

D=676+108=784;28²

D>0

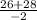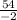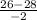x1= $\frac{26+28}{-2}$ = $\frac{54}{-2}$ = -27

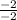x2= $\frac{26-28}{-2}$ = $\frac{-2}{-2}$ =1

Так как у нас получилось два корня, нужно подставить получившиеся значение в исходное выражение и найти верный ответ.

а) Возьмём первый корень, равный -27 и подставим в изначальное выражение.

$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$

$\frac{-27+2}{-27+3+4}$ - $\frac{-27}{-27+3}$ = $\frac{1}{8}$

$\frac{-25}{-20}$ - $\frac{-27}{-24}$ = $\frac{1}{8}$

$\frac{25}{20}$ - $\frac{27}{24}$ = $\frac{1}{8}$

$\frac{5}{4}$ - $\frac{27}{24}$ = $\frac{30}{24}$ - $\frac{27}{24}$ = $\frac{3}{24}$

$\frac{3}{24}$ = $\frac{1}{8}$ ⇒ Корень -27 подходит. Значит изначальная дробь равна $\frac{27}{24}$ = $\frac{9}{8}$ =1 $\frac{1}{8}$

б) Возьмём второй корень, равный 1 и подставим в изначальное уравнение

$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$

$\frac{1+2}{1+7}$ - $\frac{1}{1+3}$ = $\frac{1}{8}$

$\frac{3}{8}$ - $\frac{1}{4}$ = $\frac{1}{8}$

$\frac{3}{8}$ - $\frac{2}{8}$ = $\frac{1}{8}$ ⇒ Корень 1 также подходит. Значит исходное уравнение равно $\frac{1}{4}$

Так как при проверке оба корня оказались верны, то в ответе будет две дроби.

2) $\left[\begin{array}{ccc}S&U&t\\200&x&\\200&x+10&\end{array}\right]$

Рассмотрим движение машины в двух случаях: Как она должна была двигаться изначально и как она двигалась в итоге. Путь, пройденный автомобилем, не изменился. Скорость увеличилась на 10 км/ч. Так как автомобиль прибыл быстрее запланированного, то разница между временем, затраченным в первом случае, и временем, затраченным во втором случае, будет равна 1 часу. Составим уравнение.

$\frac{200}{x}$ - $\frac{200}{x+10}$ =1 Избавимся от дробей, умножив каждое число на x·(x+10)