Найдем все такие целые n, при котором неравенство выполняется.
Решать будем так:
Заметим, что не имеет целых корней. Однако он больше 0, если и меньше 0, если (так как решаем в целых числах нам этого достаточно).
Если , то для того, чтобы неравенство выполнялось, , значит , а так как решаем в целых числах, то можно написать . Найдем пересечение с и сделаем вывод, что такой случай невозможен.
Если , то , а значит , т.е. в нашем случае . Найдем пересечение и сделаем вывод, что .
Для каждого n найдем x и проверим будет ли он натуральным числом:
ответ (6;5)
Для решение уравнения предлагаю следующий
Объяснение:
Введем целый коэффициент n такой, что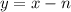 .
.
Выполним подстановку:
Упростим выражение:
Решим уравнение относительно x:
Тогда корни равны:
Очевидно, что уравнение имеет корни только, если
Найдем все такие целые n, при котором неравенство выполняется.
Решать будем так:
Заметим, что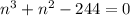 не имеет целых корней. Однако он больше 0, если
не имеет целых корней. Однако он больше 0, если 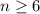 и меньше 0, если
и меньше 0, если 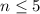 (так как решаем в целых числах нам этого достаточно).
(так как решаем в целых числах нам этого достаточно).
Если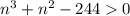 , то для того, чтобы неравенство выполнялось,
, то для того, чтобы неравенство выполнялось, 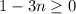 , значит
, значит 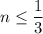 , а так как решаем в целых числах, то можно написать
, а так как решаем в целых числах, то можно написать 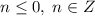 . Найдем пересечение с
. Найдем пересечение с 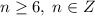 и сделаем вывод, что такой случай невозможен.
и сделаем вывод, что такой случай невозможен.
Если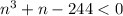 , то
, то 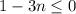 , а значит
, а значит 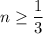 , т.е. в нашем случае
, т.е. в нашем случае  . Найдем пересечение и сделаем вывод, что
. Найдем пересечение и сделаем вывод, что 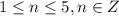 .
.
Для каждого n найдем x и проверим будет ли он натуральным числом:
При n=1:
Здесь подходит только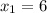 .
.
При этом x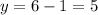 .
.
Получили пару чисел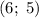 .
.
При n=2:
Ни один x не подходит.
При всех остальных n ни один x также не подходит.
Поэтому ответом будет являться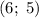 .
.
Задание выполнено!