Разобьем данное уравнение на две функции , график функции уже построен на рисунке, так что объяснять как строить такой график не буду. График функции представляет собой прямую совпадающую (при a=0) с осью абсцисс или параллельной ей (при a≠0). Тогда "передвигая" прямую можем с графика ответить на вопросы к заданию. 1) не имеет решений при a<1. 2) Из графика видно что данное уравнение имеет одно, два, или ни одного решения.
3) имеет бесконечно много решение при a=1. 4) имеет два решения при a>1.
Объяснение:
y^3=(x-1)^2 *(x-3), y=корень кубический из (x^2-2x+1)(x-3)= (корень кубический обозначу V), y=V(x^3-3x^2-2x^2+6x+x-3)=
V(x^3 -5x^2 +7x -3) (^ - значок степени), y=(x^3 -5x^2 +7x -3)^ 1/3
берем производную по формуле x^n=n*x^(n-1),, но это сложная функция.
y'=1/3 *(x^3-5x^2+7x-3)^ (-2/3) *(3x^2-10x+7)=(3x^2-10x+7)/3(x^3-5x^2+7x_3)^ 2/3 =(3x^2-10x+7)/корень кубический и под корнем (x^3-5x^2+7x-3)^2,
y'=0 когда числитель = 0, 3x^2-10x+7=0, x1=1, x2=7/3 -критические точки
+ + + + + +[1] - - - - - - - - [7/3] + + + + + + , 1-точка max, 7/3 -точка min
Разобьем данное уравнение на две функции , график функции уже построен на рисунке, так что объяснять как строить такой график не буду. График функции представляет собой прямую совпадающую (при a=0) с осью абсцисс или параллельной ей (при a≠0). Тогда "передвигая" прямую можем с графика ответить на вопросы к заданию. 1) не имеет решений при a<1. 2) Из графика видно что данное уравнение имеет одно, два, или ни одного решения.
3) имеет бесконечно много решение при a=1. 4) имеет два решения при a>1.
ОТВЕТ: 1) 2)
2) 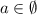 3)
3) 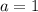 4)
4) 