Решите дробно-рациональные уравнения ​

1)

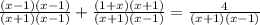
Область определения: x ≠ -1; x ≠ 1

(x - 1)^2 + (x + 1)^2 = 4

x^2 - 2x + 1 + x^2 + 2x + 1 - 4 = 0

2x^2 - 2 = 0

2(x^2 - 1) = 0

2(x + 1)(x - 1) = 0

x1 = -1; x2 = 1

Оба корня не подходят по области определения.

Решений нет.

2)

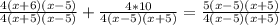
Область определения: x ≠ -5; x ≠ 5

4(x^2 + x - 30) + 40 = 5(x^2 - 25)

4x^2 + 4x - 120 + 40 = 5x^2 - 125

0 = x^2 - 4x - 45

(x - 9)(x + 5) = 0

x = -5 не подходит по области определения

x = 9 подходит.

3)

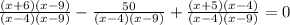
Область определения x ≠ 4; x ≠ 9

x^2 - 3x - 54 - 50 + x^2 + x - 20 = 0

2x^2 - 2x - 124 = 0

x^2 - x - 62 = 0

D = 1 - 4(-62) = 249

x1 = (1 - √249)/2; x2 = (1 + √249)/2

Но я предполагаю, что в задаче опечатка, должно быть:

Тогда получается уравнение

x^2 - x - 12 = 0

(x - 4)(x + 3) = 0

Подходит только корень

x = -3