Решите это очень намера:560,561,564​

Х - скорость лодки, У - скорость течения.

Получаем систему:
48 / (Х+У) = 3;
48 / (Х-У) = 4.

48 / 3 = Х+У;
48 / 4 = Х-У.

16 = Х+У;
12 = Х-У.

16 - Х - У = 0;
12 - Х + У = 0.

16 - Х - У = 12 - Х +У

(16-12) - Х +Х - У -У = 0

4 - 2У = 0

4 = 2У

У = 2

Отсюда (подставив в любое из уравнений системы) находим Х:

16 = Х+У
16 = Х+2
Х = 16-2
Х=14

ответ: Скорость лодки - 14 км/ч, скорость течения - 2 км/ч

Я думаю что надо решать так)

 №2

а) 2х+у=4
3х-2у=-9

 2х=4-у

х=(4-у):2

3х=-9+2у

х=(-9+2у):3

-это подставляешь в первое, ну а дальше решаеть просто)

Надо взять такие числа, которые будут максимально равны между собой и при этом будут являться целыми.

Эти числа 9 и 9.

Проверим по квадратам:

81 + 81 = 162

Теперь проверим другие числа. Один множитель уменьшим на единицу, а другой увеличим на единицу:

64 + 100 = 164

Как видим сумма получилась больше предыдущей. Возьмём еще:

9 + 729 = 738

Значительно больше первой суммы. Вывод:

надо уравнять множители, чтобы получить наименьшую сумму квадратов этих множителей.

 ответ: 81 = 9 * 9, т.к.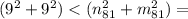 

162 < суммы квадратов множителей (при "n" </> 9, "m" </> 9).

*n81^2 - квадрат множителя 81.