ответ: 8) n=4 или n=5
Объяснение:
дробь правильная, если числитель меньше знаменателя...
n²-n+15 < 7n+3
n²-8n+12 < 0 корни по т.Виета (2) и (6);
решение "между корнями": n ∈ (2; 6),
т.е. n∈N (по условию) может быть равно: {3; 4; 5}
остальное (сократима ли дробь) проще посчитать...
n=3: дробь сократима...
n=4: дробь НЕсократима (31-простое число))
n=5: дробь НЕсократима...
решение задачи 9) на рисунке...
таких окружностей две...
касание может быть как внутренним, так и внешним...
точки касания окружностей лежат на линии центров...
ответ: 8) n=4 или n=5
Объяснение:
дробь правильная, если числитель меньше знаменателя...
n²-n+15 < 7n+3
n²-8n+12 < 0 корни по т.Виета (2) и (6);
решение "между корнями": n ∈ (2; 6),
т.е. n∈N (по условию) может быть равно: {3; 4; 5}
остальное (сократима ли дробь) проще посчитать...
n=3: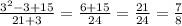
дробь сократима...
n=4: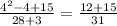
дробь НЕсократима (31-простое число))
n=5: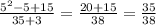
дробь НЕсократима...
решение задачи 9) на рисунке...
таких окружностей две...
касание может быть как внутренним, так и внешним...
точки касания окружностей лежат на линии центров...
2.=3x^4-12x^2+18x
3.=28a^2b+24ab^2+2a^2b-16ab^2=30a^2+8ab^2
2).=12m+20m^2-60m-20m^2=-48m
m=-0.2
-48*(-0.2)=9.6
3).1.=5a(a-4b)
2.=7x^3(1-2x^2)
3.=2ab(3ab-4a+6b)
4).1.x^2-3x=0
x(x-3)=0
x=0 или x-3=0
x=3
2.(x-2)(x+5)=0
x-2=0 или x+5=0
x=2 x=-5
3).(18xy+6x)+(-24y-8)=6x(3y+1)-8(3y+1)=(3y+1)(6x-8)
(3*0,45+1)(6*5/3-8)=2,35*2=4,7
4).1.=3(a-b)+x(a-b)=(a-b)(3+x)
2.=(a+b)^2+(3a+3b)=(a+b)^2+3(a+b)=(a+b)(a+b+3)
3.=(x^8-4X^5)+(X^3-4)=X^5(X^3-4)+(X^3-4)=(x^3-4)(x^5+1)