Если знаменатель дроби — квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный на квадратный корень, находящийся в знаменателе (это, конечно, не всегда, точнее сказать, надо умножить на такое число, чтобы при перемножении знаменателя с ним убирался корень)
1)
2)
3) вот здесь, как раз-то число, на которое умножаем, это не совсем знаменатель, но именно при перемножении с ним, мы можем избавиться от иррациональности.
Ну, вроде непонятные моменты объяснила, можно только о коэффициентах пару слов сказать :
Коэффицие́нт — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
Объяснение:
Действуем по такому методу:
Если знаменатель дроби — квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный на квадратный корень, находящийся в знаменателе (это, конечно, не всегда, точнее сказать, надо умножить на такое число, чтобы при перемножении знаменателя с ним убирался корень)
1)
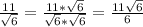
2)
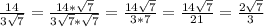
3)
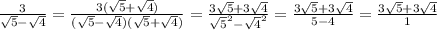вот здесь, как раз-то число, на которое умножаем, это не совсем знаменатель, но именно при перемножении с ним, мы можем избавиться от иррациональности.
P.S. если решил правильно, отметь как лучший)
1)(х-3)^2+5х-х^3+х(х-7)-12х^2+х^2(х-1)=х^2-6х+9+5х-х^3+х^2-7х-12х^2+х^3-х^2= -11х^2-8х-9
Значит сумма коэффициентов будет равна:
-11-8+9= -10
Объяснение:
Здесь нужно использовать следующие формулы :
Формула 1
(х+у) ^2=х^2+2ху+у^2
( Это нужно для части (х-3)^2 =х^2-6х+9)
Формула 2
а(b+c)=ab+ac
(Это нужно для частей х(х-7) ; х^2(х-1))
Ну, вроде непонятные моменты объяснила, можно только о коэффициентах пару слов сказать :
Коэффицие́нт — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
Теперь точно все. Удачки