Значение производной в точке касания равно угловому коэффициенту касательной, в данном случай двум. Значит абсцисса точки касания находится из уравнения:
Т.о. имеются две точки, в которых касательная к графику нашей функции имеет угловой коэффициент, равный 2. Вычислим значения функции в этих точках и проверим, удовлетворяют ли они уравнению касательной:
при х = -1 при
Проверим удовлетворяет ли уравнению касательной у=2х точка (-1;-2): -2 = 2*(-1) -2 = -2 ( ДА)
Проверим удовлетворяет ли уравнению касательной у=2х точка : (НЕТ)
Нехай за год перший робітник виконає завдання, а за
год перший робітник виконає завдання, а за 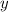 год — другий. Тоді за одну годину перший робітник виконає
год — другий. Тоді за одну годину перший робітник виконає  усього завдання, а другий робітник —
усього завдання, а другий робітник —  .
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто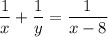
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто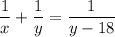
Складаємо систему з двох рівнянь:
Тут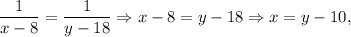 оскільки ліві частини рівнянь рівні.
оскільки ліві частини рівнянь рівні.
Підставимо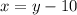 в перше рівняння:
в перше рівняння:
Якщо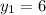 , то
, то 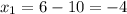 — не відповідає сенсу задачі.
— не відповідає сенсу задачі.
Якщо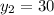 , то
, то 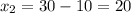
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.
Т.о. имеются две точки, в которых касательная к графику нашей функции имеет угловой коэффициент, равный 2. Вычислим значения функции в этих точках и проверим, удовлетворяют ли они уравнению касательной:
при х = -1
при
Проверим удовлетворяет ли уравнению касательной у=2х точка (-1;-2):
-2 = 2*(-1)
-2 = -2 ( ДА)
Проверим удовлетворяет ли уравнению касательной у=2х точка
ответ: абсцисса точки касания равна -1.