Это из третьей строки вычли первую строку. Дальше вычтем из 1 строки вторую, получим матрицу вида
Матрица получилась нижнетреугольная. Ранг матрицы равено количеству линейнонезависимых строк или столбцов в матрице.
Рассмотрим при каких а в матрице появляются нулевые строки
1. а+1=0, а=-1, в этом случаем третья строка зануляется и можно занулить второй столбец. Вычеркиваем нулевую строку и столбец, получаем диагональную матрицу размером 2х2. Количество линейнонезависимых строк=2 значит Rg(A)=2
2. a=0. Получается матрица вида
Видно, что вторая и третья строки линейно зависимы (2 получается из третьей домножением на -1). Действуя так же как и в случае 1, получаем матрицу 2х2 с линейнонезависимыми строками, значит Rg(A)=2
Во всех остальных случаев ранг матрицы получается равен Rg(A)=3.
Т.к при любых других значениях а матрица имеет диагональный вид. Значит количество линейнонезависимых векторов будет равно 3.
Это из третьей строки вычли первую строку. Дальше вычтем из 1 строки вторую, получим матрицу вида
Матрица получилась нижнетреугольная. Ранг матрицы равено количеству линейнонезависимых строк или столбцов в матрице.
Рассмотрим при каких а в матрице появляются нулевые строки
1. а+1=0, а=-1, в этом случаем третья строка зануляется и можно занулить второй столбец. Вычеркиваем нулевую строку и столбец, получаем диагональную матрицу размером 2х2. Количество линейнонезависимых строк=2 значит Rg(A)=2
2. a=0. Получается матрица вида
Во всех остальных случаев ранг матрицы получается равен Rg(A)=3.
Т.к при любых других значениях а матрица имеет диагональный вид. Значит количество линейнонезависимых векторов будет равно 3.
ответ: a=-1 и a=0 Rg(A)=2 ,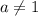 и ф
и ф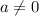 Rg(A)=3
Rg(A)=3
( 2a + 4b) - b( a + 2b) = 2( a + 2b) - b( a + 2b) = ( a + 2b)(2 - b)
x^2 - 64y^2= ( x - 8y)(x + 8y)
2) ( 7m -n)(7m + n) / 3mn( n - 7m) = - (7m + n) / 3mn = - 7m -n / 3mn
(9x - 4)(9x + 4) / ( 4 + 9x)^2 = (9x - 4)(9x + 4) / (4 + 9x)(4 + 9x) =(9x - 4)/(9x+4)
3) ( x - 4)^2 - 25 = 0
( x - 4 - 5)(x - 4 + 5) = 0
( x - 9)(x + 1) = 0
x - 9= 0
x = 9
x + 1 =0
x = - 1
4) x^2 - 12x - 45 = ( x - 15)(x + 3)
x^2 - 12x - 45 = x^2 + 3x - 15x - 45
x^2 - 12x - 45 = x^2 - 12x - 45 - верно,тождество доказано
5) (99 - 61)(99^2 + 99*61 + 61^2) / 38 + 99*61 = 38*19561 / 6077=
= 122,3166