Алгебра: Решите квадратное уравнение

Решите квадратное уравнение

Показать ответ

Ответ:

kaskovam

17.02.2020 01:54

Відповідь:

Пояснення:

Нехай перше та друге числа — x та y відповідно. Отже, числа x, y і 12 утворюють геометричну прогресію, а числа x, y і -36 — арифметичну.

Скористаємося основними властивостями цих прогресій. Квадрат кожного члена геометричної дорівнює добутку сусідніх. Зокрема для члена y,

$y^2=12x \; (*)$

Кожен член арифметичної прогресії дорівнює середньому арифметичному сусідніх. Зокрема для того ж члена y,

$y=\frac{x-36}{2}$ .

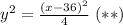Звідси $y^2=\frac{(x-36)^2}{4} \; (**)$ .

Ліві частини рівнянь (*) і (**) збігаються, тому прирівняємо праві та знайдемо x:

$12x=\frac{(x-36)^2}{4}\\48x=(x-36)^2\\48x=x^2-72x+1296\\x^2-120x+1296=0\\D_1=k^2-ac=(-60)^2-1296=3600-1296=2304\\x=\frac{-k\pm \sqrt{D_1}}{a}\\\begin{cases} x_1=\frac{60+\sqrt{2304} }{1}=60+48=108\\x_2=\frac{60-\sqrt{2304} }{1}=60-48=12 \end{cases}$

Якщо перше з розглядуваних чисел — 12, то друге дорівнює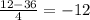 $\frac{12-36}{4}=-12$ . Воно не натуральне й не задовольняє умові. Якщо ж x=108, то 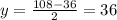$y=\frac{108-36}{2}=36$ , що цілком відповідає умові задачі.

Тоді сума цифр першого числа 1+0+8=9.

0,0(0 оценок)

Ответ:

Еленаелец77

09.04.2022 18:24

1 - В, 2 - А, 3 - Д, 4 - Б.

Объяснение:

Определить четную и нечетную функцию можно так: если функция симметрична оси ординат (ось у) то это функция четная, если симметрична относительно начала координат (0,0) то эта функция нечетная.

Сразу видно, что рис. 4 симметрична относительно оси ординат и является четной, а рис. 1 симметрична относительно начала координат и является нечетной.

Нулем функции называют место, где функция пересекает ось абсцисс (ось х), функция на рис. 3 пересекает как раз трижды.

И локальный экстремум - это максимальное или минимальное значение функции на определенной ее части. На рис. 2 как раз видно два таких значения.

0,0(0 оценок)

Популярные вопросы: Алгебра